Question
Solve the equation
x=1
Evaluate
4(5x−101)=52
Multiply the terms
More Steps


Evaluate
4(5x−101)
Use the the distributive property to expand the expression
4×5x+4(−101)
Multiply the terms
54x+4(−101)
Multiply the numbers
More Steps


Evaluate
4(−101)
Multiplying or dividing an odd number of negative terms equals a negative
−4×101
Reduce the numbers
−2×51
Multiply the numbers
−52
54x−52
54x−52=52
Move the constant to the right-hand side and change its sign
54x=52+52
Add the numbers
More Steps


Evaluate
52+52
Write all numerators above the common denominator
52+2
Add the numbers
54
54x=54
Multiply both sides of the equation by 5
54x×5=54×5
Multiply the terms
4x=4
Divide both sides
44x=44
Divide the numbers
x=44
Solution
More Steps


Evaluate
44
Reduce the numbers
11
Calculate
1
x=1
Show Solution

Rewrite the equation
x=1
Evaluate
4(5x−101)=52
Evaluate
More Steps


Evaluate
4(5x−101)
Subtract the terms
More Steps


Simplify
5x−101
Reduce fractions to a common denominator
5×2x×2−101
Multiply the numbers
10x×2−101
Write all numerators above the common denominator
10x×2−1
Use the commutative property to reorder the terms
102x−1
4×102x−1
Cancel out the common factor 2
2×52x−1
Multiply the terms
52(2x−1)
52(2x−1)=52
Reduce the fraction
More Steps


Evaluate
52(2x−1)
Calculate
54x−2
Reduce the fraction
54x−52
54x−52=52
Multiply both sides of the equation by LCD
4x−2=2
Move the constant to the right side
4x=4
Solution
x=1
Show Solution

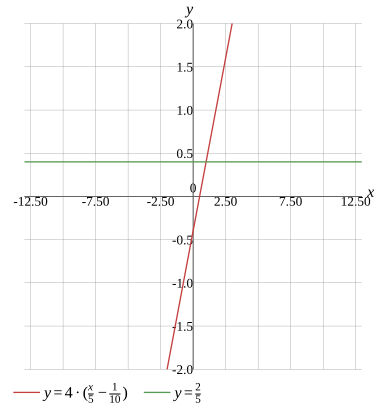
Graph