Question
Solve the equation(The real numbers system)
x∈/R
Evaluate
4x4−4(x−4)=x
Move the expression to the left side
4x4−4(x−4)−x=0
Calculate
More Steps


Evaluate
4x4−4(x−4)−x
Expand the expression
More Steps


Calculate
−4(x−4)
Apply the distributive property
−4x−(−4×4)
Multiply the numbers
−4x−(−16)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
−4x+16
4x4−4x+16−x
Subtract the terms
More Steps


Evaluate
−4x−x
Collect like terms by calculating the sum or difference of their coefficients
(−4−1)x
Subtract the numbers
−5x
4x4−5x+16
4x4−5x+16=0
Solution
x∈/R
Show Solution

Solve the equation(The complex numbers system)
x1≈−1.005977+1.150058i,x2≈−1.005977−1.150058i,x3≈1.005977+0.837465i,x4≈1.005977−0.837465i
Evaluate
4x4−4(x−4)=x
Move the expression to the left side
4x4−4(x−4)−x=0
Calculate
More Steps


Evaluate
4x4−4(x−4)−x
Expand the expression
More Steps


Calculate
−4(x−4)
Apply the distributive property
−4x−(−4×4)
Multiply the numbers
−4x−(−16)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
−4x+16
4x4−4x+16−x
Subtract the terms
More Steps


Evaluate
−4x−x
Collect like terms by calculating the sum or difference of their coefficients
(−4−1)x
Subtract the numbers
−5x
4x4−5x+16
4x4−5x+16=0
Calculate
x≈1.005977−0.837465ix≈1.005977+0.837465ix≈−1.005977−1.150058ix≈−1.005977+1.150058i
Solution
x1≈−1.005977+1.150058i,x2≈−1.005977−1.150058i,x3≈1.005977+0.837465i,x4≈1.005977−0.837465i
Show Solution

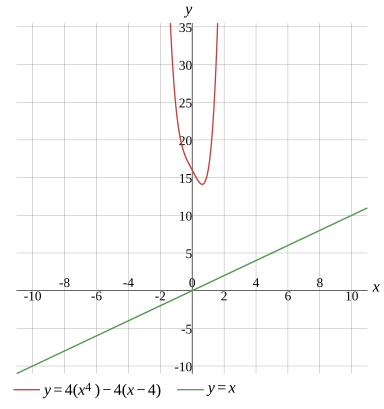
Graph