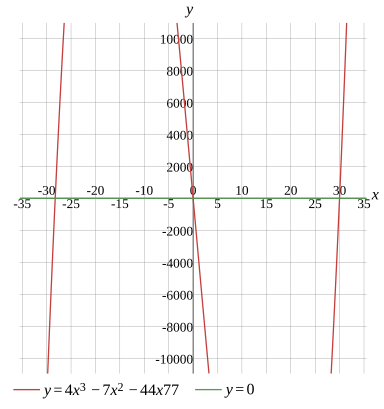
Question
Solve the equation
x1=87−54257,x2=0,x3=87+54257
Alternative Form
x1≈−28.241415,x2=0,x3≈29.991415
Evaluate
4x3−7x2−44x×77=0
Multiply the terms
4x3−7x2−3388x=0
Factor the expression
x(4x2−7x−3388)=0
Separate the equation into 2 possible cases
x=04x2−7x−3388=0
Solve the equation
More Steps


Evaluate
4x2−7x−3388=0
Substitute a=4,b=−7 and c=−3388 into the quadratic formula x=2a−b±b2−4ac
x=2×47±(−7)2−4×4(−3388)
Simplify the expression
x=87±(−7)2−4×4(−3388)
Simplify the expression
More Steps


Evaluate
(−7)2−4×4(−3388)
Multiply
(−7)2−(−54208)
Rewrite the expression
72−(−54208)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
72+54208
Evaluate the power
49+54208
Add the numbers
54257
x=87±54257
Separate the equation into 2 possible cases
x=87+54257x=87−54257
x=0x=87+54257x=87−54257
Solution
x1=87−54257,x2=0,x3=87+54257
Alternative Form
x1≈−28.241415,x2=0,x3≈29.991415
Show Solution

Graph