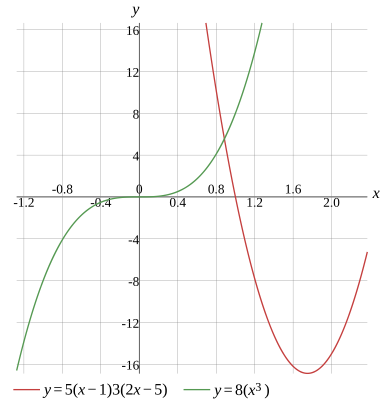
Question
Solve the equation(The real numbers system)
x≈0.885375
Evaluate
5(x−1)×3(2x−5)=8x3
Evaluate
15(x−1)(2x−5)=8x3
Expand the expression
More Steps


Evaluate
15(x−1)(2x−5)
Multiply the terms
More Steps


Evaluate
15(x−1)
Apply the distributive property
15x−15×1
Any expression multiplied by 1 remains the same
15x−15
(15x−15)(2x−5)
Apply the distributive property
15x×2x−15x×5−15×2x−(−15×5)
Multiply the terms
More Steps


Evaluate
15x×2x
Multiply the numbers
30x×x
Multiply the terms
30x2
30x2−15x×5−15×2x−(−15×5)
Multiply the numbers
30x2−75x−15×2x−(−15×5)
Multiply the numbers
30x2−75x−30x−(−15×5)
Multiply the numbers
30x2−75x−30x−(−75)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
30x2−75x−30x+75
Subtract the terms
More Steps


Evaluate
−75x−30x
Collect like terms by calculating the sum or difference of their coefficients
(−75−30)x
Subtract the numbers
−105x
30x2−105x+75
30x2−105x+75=8x3
Move the expression to the left side
30x2−105x+75−8x3=0
Solution
x≈0.885375
Show Solution

Solve the equation(The complex numbers system)
x1≈1.432312−2.921851i,x2≈1.432312+2.921851i,x3≈0.885375
Evaluate
5(x−1)×3(2x−5)=8x3
Multiply the terms
15(x−1)(2x−5)=8x3
Expand the expression
More Steps


Evaluate
15(x−1)(2x−5)
Multiply the terms
More Steps


Evaluate
15(x−1)
Apply the distributive property
15x−15×1
Any expression multiplied by 1 remains the same
15x−15
(15x−15)(2x−5)
Apply the distributive property
15x×2x−15x×5−15×2x−(−15×5)
Multiply the terms
More Steps


Evaluate
15x×2x
Multiply the numbers
30x×x
Multiply the terms
30x2
30x2−15x×5−15×2x−(−15×5)
Multiply the numbers
30x2−75x−15×2x−(−15×5)
Multiply the numbers
30x2−75x−30x−(−15×5)
Multiply the numbers
30x2−75x−30x−(−75)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
30x2−75x−30x+75
Subtract the terms
More Steps


Evaluate
−75x−30x
Collect like terms by calculating the sum or difference of their coefficients
(−75−30)x
Subtract the numbers
−105x
30x2−105x+75
30x2−105x+75=8x3
Move the expression to the left side
30x2−105x+75−8x3=0
Calculate
x≈0.885375x≈1.432312+2.921851ix≈1.432312−2.921851i
Solution
x1≈1.432312−2.921851i,x2≈1.432312+2.921851i,x3≈0.885375
Show Solution

Graph