Solve 5x^2-50x=-60

Evaluate

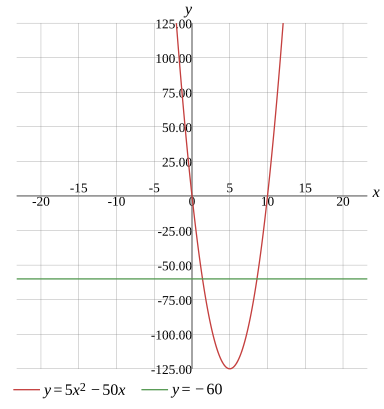
5 x^{2} - 50 x = - 60

Move the expression to the left side

5 x^{2} - 50 x + 60 = 0

Substitute a= 5,b= - 50 and c= 60 into the quadratic formula x = \frac{- b \pm b ^{2} - 4 a c}{2 a}

x = \frac{50 \pm ( - 50 ) ^{2} - 4 \times 5 \times 60}{2 \times 5}

Simplify the expression

x = \frac{50 \pm ( - 50 ) ^{2} - 4 \times 5 \times 60}{10}

Simplify the expression

More Steps

x = \frac{50 \pm 1300}{10}

Simplify the radical expression

More Steps

x = \frac{50 \pm 10 13}{10}

Separate the equation into 2 possible cases

x = \frac{50 + 10 13}{10} x = \frac{50 - 10 13}{10}

Simplify the expression

More Steps

x = 5 + 13 x = \frac{50 - 10 13}{10}

Simplify the expression

More Steps

x = 5 + 13 x = 5 - 13

Solution

x_{1} = 5 - 13, x_{2} = 5 + 13

Alternative Form

x_{1} \approx 1.394449, x_{2} \approx 8.605551

Solve the quadratic equation