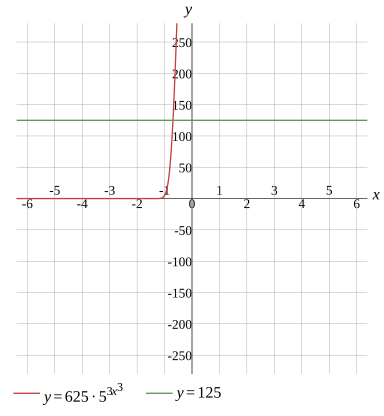
Question
Solve the equation
x=−339
Alternative Form
x≈−0.693361
Evaluate
625×53x3=125
Multiply the terms
More Steps


Evaluate
625×53x3
Rewrite the expression
54×53x3
Calculate
53x3+4
53x3+4=125
Rewrite in exponential form
53x3+4=53
Since the bases are the same,set the exponents equal
3x3+4=3
Move the constant to the right-hand side and change its sign
3x3=3−4
Subtract the numbers
3x3=−1
Divide both sides
33x3=3−1
Divide the numbers
x3=3−1
Use b−a=−ba=−ba to rewrite the fraction
x3=−31
Take the 3-th root on both sides of the equation
3x3=3−31
Calculate
x=3−31
Solution
More Steps


Evaluate
3−31
An odd root of a negative radicand is always a negative
−331
To take a root of a fraction,take the root of the numerator and denominator separately
−3331
Simplify the radical expression
−331
Multiply by the Conjugate
33×332−332
Simplify
33×332−39
Multiply the numbers
More Steps


Evaluate
33×332
The product of roots with the same index is equal to the root of the product
33×32
Calculate the product
333
Reduce the index of the radical and exponent with 3
3
3−39
Calculate
−339
x=−339
Alternative Form
x≈−0.693361
Show Solution

Graph