Solve 7sina 13cosa/5sina-17cosa=3

Evaluate

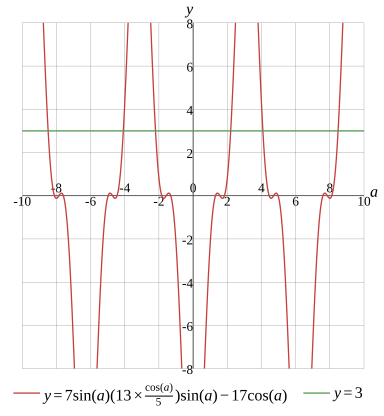
7 sin (a) (13 \times \frac{cos ( a )}{5}) sin (a) - 17 cos (a) = 3

Remove the parentheses

7 sin (a) \times 13 \times \frac{cos ( a )}{5} sin (a) - 17 cos (a) = 3

Multiply

More Steps

\frac{91 sin ^{2} ( a ) cos ( a )}{5} - 17 cos (a) = 3

Use sin^{2} (x) = 1 - cos^{2} (x) to rewrite the expression

\frac{6 cos ( a ) - 91 cos ^{3} ( a )}{5} = 3

Cross multiply

6 cos (a) - 91 cos^{3} (a) = 5 \times 3

Simplify the equation

6 cos (a) - 91 cos^{3} (a) = 15

Move the expression to the left side

6 cos (a) - 91 cos^{3} (a) - 15 = 0

Calculate

cos (a) \approx - 0.588316

Use the inverse trigonometric function

a = arccos (- 0.588316)

Calculate

a = - arccos (- 0.588316) a = arccos (- 0.588316)

Add the period of 2 kπ, k \in Z to find all solutions

a = - arccos (- 0.588316) + 2 kπ, k \in Z a = arccos (- 0.588316) + 2 kπ, k \in Z

Solution

a = {- arccos (- 0.588316) + 2 kπ arccos (- 0.588316) + 2 kπ, k \in Z

Alternative Form

a \approx {- 2.199771 + 2 kπ 2.199771 + 2 kπ, k \in Z

Alternative Form

a \approx {- 126.03758 4^{\circ} + 36 0^{\circ} k 126.03758 4^{\circ} + 36 0^{\circ} k, k \in Z

Solve the equation