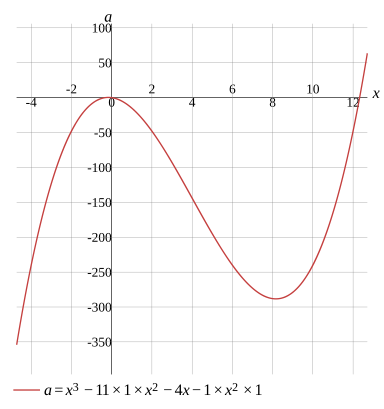
Solve a = x^3-11*1 x^2-4x-1 x^2*1

Evaluate

a = x^{3} - 11 \times 1 \times x^{2} - 4 x - 1 \times x^{2} \times 1

Simplify

More Steps

a = x^{3} - 12 x^{2} - 4 x

Take the derivative of both sides

a^{'} = \frac{d}{d x} (x^{3} - 12 x^{2} - 4 x)

Use differentiation rule \frac{d}{d x} (f (x) \pm g (x)) = \frac{d}{d x} (f (x)) \pm \frac{d}{d x} (g (x))

a^{'} = \frac{d}{d x} (x^{3}) - \frac{d}{d x} (12 x^{2}) - \frac{d}{d x} (4 x)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

a^{'} = 3 x^{2} - \frac{d}{d x} (12 x^{2}) - \frac{d}{d x} (4 x)

Calculate

More Steps

a^{'} = 3 x^{2} - 24 x - \frac{d}{d x} (4 x)

Solution

More Steps

a^{'} = 3 x^{2} - 24 x - 4

Function