Solve a^2-14a^44=-3

Question

Solve the equation

a_{1} = - \frac{7 + 7 673}{28}, a_{2} = \frac{7 + 7 673}{28}

Alternative Form

a_{1} \approx - 0.490465, a_{2} \approx 0.490465

Evaluate

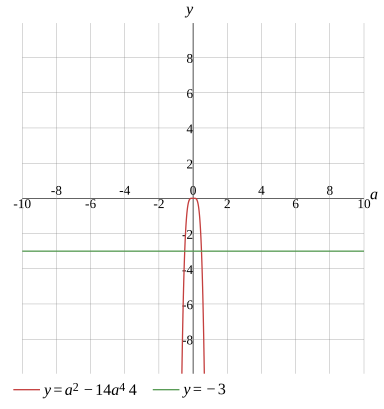
a^{2} - 14 a^{4} \times 4 = - 3

Multiply the terms

a^{2} - 56 a^{4} = - 3

Move the expression to the left side

a^{2} - 56 a^{4} - (- 3) = 0

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

a^{2} - 56 a^{4} + 3 = 0

Solve the equation using substitution t = a^{2}

t - 56 t^{2} + 3 = 0

Rewrite in standard form

- 56 t^{2} + t + 3 = 0

Multiply both sides

56 t^{2} - t - 3 = 0

Substitute a= 56,b= - 1 and c= - 3 into the quadratic formula t = \frac{- b \pm b ^{2} - 4 a c}{2 a}

t = \frac{1 \pm ( - 1 ) ^{2} - 4 \times 56 ( - 3 )}{2 \times 56}

Simplify the expression

t = \frac{1 \pm ( - 1 ) ^{2} - 4 \times 56 ( - 3 )}{112}

Simplify the expression

More Steps

t = \frac{1 \pm 673}{112}

Separate the equation into 2 possible cases

t = \frac{1 + 673}{112} t = \frac{1 - 673}{112}

Substitute back

a^{2} = \frac{1 + 673}{112} a^{2} = \frac{1 - 673}{112}

Solve the equation for a

More Steps

a = \frac{7 + 7 673}{28} a = - \frac{7 + 7 673}{28} a^{2} = \frac{1 - 673}{112}

Since the left-hand side is always positive or 0,and the right-hand side is always negative,the statement is false for any value of a

a = \frac{7 + 7 673}{28} a = - \frac{7 + 7 673}{28} a \in / R

Find the union

a = \frac{7 + 7 673}{28} a = - \frac{7 + 7 673}{28}

Solution

a_{1} = - \frac{7 + 7 673}{28}, a_{2} = \frac{7 + 7 673}{28}

Alternative Form

a_{1} \approx - 0.490465, a_{2} \approx 0.490465

Show Solution

Solve the equation

Graph