Solve b=(4x-5)*(x^2)-(x^5)*(x - 5) - 3x ^ 2 - x - ScanMath

HOME CALCULATOR

DOWNLOAD FOR FREE

Algebra
Calculus
Trigonometry
Matrix

Type your math problem... b=(4x-5)*(x^2)-(x^5)*(x - 5) - 3x ^ 2 - x

Question

Function

Evaluate the derivative

solver-selected-icon

Find the domain

Find the y-intercept

Load more

b^{'} = 12 x^{2} - 16 x - 6 x^{5} + 25 x^{4} - 1

Evaluate

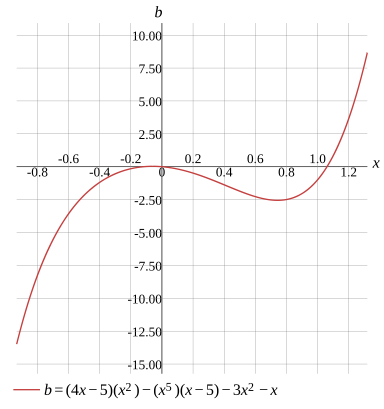
b = (4 x - 5) x^{2} - x^{5} (x - 5) - 3 x^{2} - x

Simplify

More Steps

b = 4 x^{3} - 8 x^{2} - x^{6} + 5 x^{5} - x

Take the derivative of both sides

b^{'} = \frac{d}{d x} (4 x^{3} - 8 x^{2} - x^{6} + 5 x^{5} - x)

Use differentiation rule \frac{d}{d x} (f (x) \pm g (x)) = \frac{d}{d x} (f (x)) \pm \frac{d}{d x} (g (x))

b^{'} = \frac{d}{d x} (4 x^{3}) - \frac{d}{d x} (8 x^{2}) - \frac{d}{d x} (x^{6}) + \frac{d}{d x} (5 x^{5}) - \frac{d}{d x} (x)

Calculate

More Steps

b^{'} = 12 x^{2} - \frac{d}{d x} (8 x^{2}) - \frac{d}{d x} (x^{6}) + \frac{d}{d x} (5 x^{5}) - \frac{d}{d x} (x)

Calculate

More Steps

b^{'} = 12 x^{2} - 16 x - \frac{d}{d x} (x^{6}) + \frac{d}{d x} (5 x^{5}) - \frac{d}{d x} (x)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

b^{'} = 12 x^{2} - 16 x - 6 x^{5} + \frac{d}{d x} (5 x^{5}) - \frac{d}{d x} (x)

Calculate

More Steps

b^{'} = 12 x^{2} - 16 x - 6 x^{5} + 25 x^{4} - \frac{d}{d x} (x)

Solution

b^{'} = 12 x^{2} - 16 x - 6 x^{5} + 25 x^{4} - 1

Show Solution

Solve the equation

b = 4 x^{3} - 8 x^{2} - x^{6} + 5 x^{5} - x

Show Solution

Graph

Graph