Algebra
Calculus
Trigonometry
Matrix
Question
Solve the equation
θ=8π+2kπ,k∈Z
Alternative Form
θ=22.5∘+90∘k,k∈Z
Alternative Form
θ≈0.392699+2kπ,k∈Z
Evaluate
cos(2θ)=sin(2θ)×1
Any expression multiplied by 1 remains the same
cos(2θ)=sin(2θ)
Divide both sides
sin(2θ)cos(2θ)=1
Divide the terms
More Steps
Evaluate
sin(2θ)cos(2θ)
Rewrite the expression
sin−1(2θ)cos(2θ)
Rewrite the expression
cot(2θ)
cot(2θ)=1
Use the inverse trigonometric function
2θ=arccot(1)
Calculate
2θ=4π
Add the period of kπ,k∈Z to find all solutions
2θ=4π+kπ,k∈Z
Solution
More Steps
Evaluate
2θ=4π+kπ
Divide both sides
22θ=24π+kπ
Divide the numbers
θ=24π+kπ
Divide the numbers
θ=8π+2kπ
θ=8π+2kπ,k∈Z
Alternative Form
θ=22.5∘+90∘k,k∈Z
Alternative Form
θ≈0.392699+2kπ,k∈Z
Show Solution
Rewrite the equation
x2−y2−2yx=0
Evaluate
cos(2θ)=sin(2θ)×1
Any expression multiplied by 1 remains the same
cos(2θ)=sin(2θ)
Simplify the expression
cos2(θ)−sin2(θ)=2sin(θ)cos(θ)
Multiply both sides
(rcos(θ))2−(rsin(θ))2=2sin(θ)cos(θ)×r2
Rewrite the expression
(rcos(θ))2−(rsin(θ))2−2sin(θ)cos(θ)×r2=0
Solution
More Steps
Evaluate
(rcos(θ))2−(rsin(θ))2−2sin(θ)cos(θ)×r2
To covert the equation to rectangular coordinates using conversion formulas,substitute rcosθ for x
x2−(rsin(θ))2−2sin(θ)cos(θ)×r2
To covert the equation to rectangular coordinates using conversion formulas,substitute rsinθ for y
x2−y2−2sin(θ)cos(θ)×r2
Use substitution
More Steps
Evaluate
−2sin(θ)cos(θ)×r2
Use the commutative property to reorder the terms
r2sin(θ)cos(θ)(−2)
To covert the equation to rectangular coordinates using conversion formulas,substitute rsinθ for y
rcos(θ)×y(−2)
To covert the equation to rectangular coordinates using conversion formulas,substitute rcosθ for x
yx(−2)
Multiply the terms
−2yx
x2−y2−2yx
x2−y2−2yx=0
Show Solution
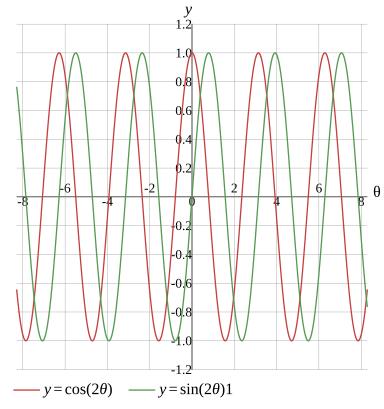
Graph
