Solve cot^2x-cscx=1 - ScanMath

HOME CALCULATOR

DOWNLOAD FOR FREE

Algebra
Calculus
Trigonometry
Matrix

Type your math problem... cot^2x-cscx=1

Question

Solve the equation

x = \frac{π}{6} + \frac{2 kπ}{3}, k \in Z

Alternative Form

x = 3 0^{\circ} + 12 0^{\circ} k, k \in Z

Alternative Form

x \approx 0.523599 + \frac{2 kπ}{3}, k \in Z

Evaluate

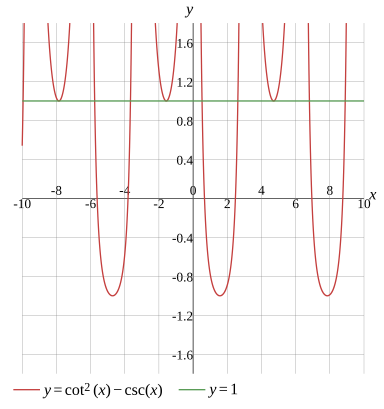
cot^{2} (x) - csc (x) = 1

Find the domain

cot^{2} (x) - csc (x) = 1, x \neq = kπ, k \in Z

Use cot^{2} (x) = csc^{2} (x) - 1 to rewrite the expression

csc^{2} (x) - 1 - csc (x) = 1

Move the expression to the left side

csc^{2} (x) - 2 - csc (x) = 0

Factor the expression

More Steps

(csc (x) - 2) (csc (x) + 1) = 0

When the product of factors equals 0,at least one factor is 0

csc (x) - 2 = 0 csc (x) + 1 = 0

Solve the equation for csc (x)

More Steps

csc (x) = 2 csc (x) + 1 = 0

Solve the equation for csc (x)

More Steps

csc (x) = 2 csc (x) = - 1

Calculate

More Steps

x = {\frac{π}{6} + 2 kπ \frac{5 π}{6} + 2 kπ, k \in Z csc (x) = - 1

Calculate

More Steps

x = {\frac{π}{6} + 2 kπ \frac{5 π}{6} + 2 kπ, k \in Z x = \frac{3 π}{2} + 2 kπ, k \in Z

Find the union

x = \frac{π}{6} + \frac{2 kπ}{3}, k \in Z

Check if the solution is in the defined range

x = \frac{π}{6} + \frac{2 kπ}{3}, k \in Z, x \neq = kπ, k \in Z

Solution

x = \frac{π}{6} + \frac{2 kπ}{3}, k \in Z

Alternative Form

x = 3 0^{\circ} + 12 0^{\circ} k, k \in Z

Alternative Form

x \approx 0.523599 + \frac{2 kπ}{3}, k \in Z

Show Solution

Graph

Graph