Algebra
Calculus
Trigonometry
Matrix
Question
Solve the equation
θ∈∅
Alternative Form
No solution
Evaluate
cot(θ)×1=csc(θ)
Find the domain
cot(θ)×1=csc(θ),θ=kπ,k∈Z
Any expression multiplied by 1 remains the same
cot(θ)=csc(θ)
Rewrite the expression
sin(θ)cos(θ)=sin(θ)1
Cross multiply
cos(θ)sin(θ)=sin(θ)
Move the expression to the left side
cos(θ)sin(θ)−sin(θ)=0
Factor the expression
More Steps
Calculate
cos(θ)sin(θ)−sin(θ)
Calculate
sin(θ)cos(θ)−sin(θ)
Factor out sin(θ) from the expression
sin(θ)(cos(θ)−1)
sin(θ)(cos(θ)−1)=0
Separate the equation into 2 possible cases
sin(θ)=0cos(θ)−1=0
Solve the equation
More Steps
Evaluate
sin(θ)=0
Use the inverse trigonometric function
θ=arcsin(0)
Calculate
θ=0
Add the period of kπ,k∈Z to find all solutions
θ=kπ,k∈Z
θ=kπ,k∈Zcos(θ)−1=0
Solve the equation
More Steps
Evaluate
cos(θ)−1=0
Move the constant to the right-hand side and change its sign
cos(θ)=0+1
Removing 0 doesn't change the value,so remove it from the expression
cos(θ)=1
Use the inverse trigonometric function
θ=arccos(1)
Calculate
θ=0
Add the period of 2kπ,k∈Z to find all solutions
θ=2kπ,k∈Z
θ=kπ,k∈Zθ=2kπ,k∈Z
Find the union
θ=kπ,k∈Z
Check if the solution is in the defined range
θ=kπ,k∈Z,θ=kπ,k∈Z
Solution
θ∈∅
Alternative Form
No solution
Show Solution
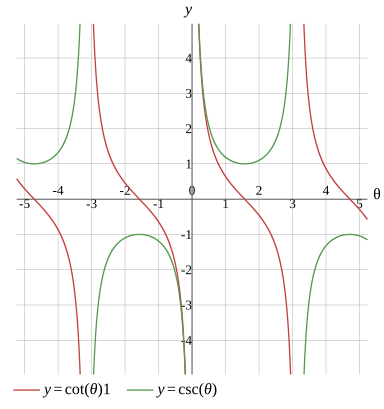
Graph
