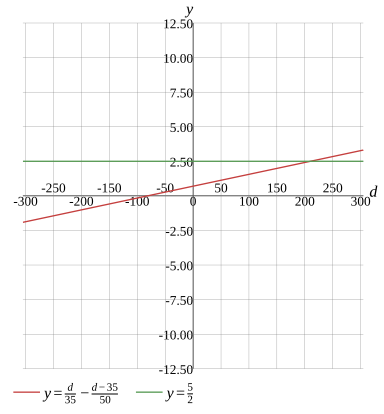
Question
Solve the equation
d=210
Evaluate
35d−50d−35=25
Multiply both sides of the equation by LCD
(35d−50d−35)×350=25×350
Simplify the equation
More Steps


Evaluate
(35d−50d−35)×350
Apply the distributive property
35d×350−50d−35×350
Simplify
d×10+(−d+35)×7
Use the commutative property to reorder the terms
10d+(−d+35)×7
Multiply the terms
More Steps


Evaluate
(−d+35)×7
Apply the distributive property
−d×7+35×7
Use the commutative property to reorder the terms
−7d+35×7
Calculate
−7d+245
10d−7d+245
Subtract the terms
More Steps


Evaluate
10d−7d
Collect like terms by calculating the sum or difference of their coefficients
(10−7)d
Subtract the numbers
3d
3d+245
3d+245=25×350
Simplify the equation
More Steps


Evaluate
25×350
Simplify
5×175
Multiply the numbers
875
3d+245=875
Move the constant to the right side
3d=875−245
Subtract the numbers
3d=630
Divide both sides
33d=3630
Divide the numbers
d=3630
Solution
More Steps


Evaluate
3630
Reduce the numbers
1210
Calculate
210
d=210
Show Solution

Graph