Algebra
Calculus
Trigonometry
Matrix
Question
Function
Find the vertex
Find the axis of symmetry
Rewrite in vertex form
Load more
(23,449)
Evaluate
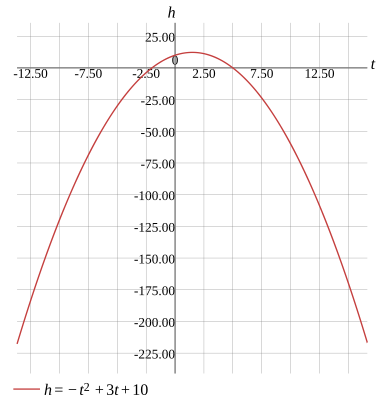
h=−t2+3t+10
Find the t-coordinate of the vertex by substituting a=−1 and b=3 into t = −2ab
t=−2(−1)3
Solve the equation for t
t=23
Find the y-coordinate of the vertex by evaluating the function for t=23
h=−(23)2+3×23+10
Calculate
More Steps
Evaluate
−(23)2+3×23+10
Multiply the numbers
More Steps
Evaluate
3×23
Multiply the numbers
23×3
Multiply the numbers
29
−(23)2+29+10
Evaluate the power
−49+29+10
Reduce fractions to a common denominator
−49+2×29×2+2×210×2×2
Multiply the numbers
−49+49×2+2×210×2×2
Multiply the numbers
−49+49×2+410×2×2
Write all numerators above the common denominator
4−9+9×2+10×2×2
Multiply the numbers
4−9+18+10×2×2
Multiply the terms
More Steps
Evaluate
10×2×2
Multiply the terms
20×2
Multiply the numbers
40
4−9+18+40
Add the numbers
449
h=449
Solution
(23,449)
Show Solution
Solve the equation
t=23+49−4ht=23−49−4h
Evaluate
h=−t2+3t+10
Swap the sides of the equation
−t2+3t+10=h
Move the expression to the left side
−t2+3t+10−h=0
Multiply both sides
t2−3t−10+h=0
Substitute a=1,b=−3 and c=−10+h into the quadratic formula t=2a−b±b2−4ac
t=23±(−3)2−4(−10+h)
Simplify the expression
More Steps
Evaluate
(−3)2−4(−10+h)
Multiply the terms
More Steps
Evaluate
4(−10+h)
Apply the distributive property
−4×10+4h
Multiply the numbers
−40+4h
(−3)2−(−40+4h)
Rewrite the expression
32−(−40+4h)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
32+40−4h
Evaluate the power
9+40−4h
Add the numbers
49−4h
t=23±49−4h
Solution
t=23+49−4ht=23−49−4h
Show Solution
Graph
