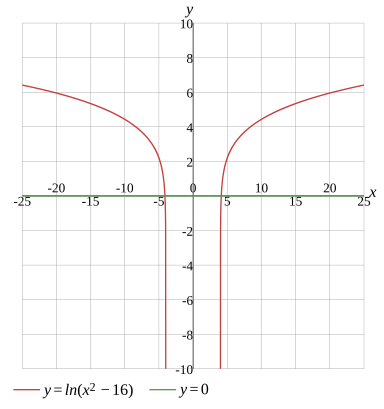
Question
Solve the equation
x1=−17,x2=17
Alternative Form
x1≈−4.123106,x2≈4.123106
Evaluate
ln(x2−16)=0
Find the domain
More Steps


Evaluate
x2−16>0
Move the constant to the right side
x2>16
Take the 2-th root on both sides of the inequality
x2>16
Calculate
∣x∣>4
Separate the inequality into 2 possible cases
x>4x<−4
Find the union
x∈(−∞,−4)∪(4,+∞)
ln(x2−16)=0,x∈(−∞,−4)∪(4,+∞)
Convert the logarithm into exponential form using the fact that logax=b is equal to x=ab
x2−16=e0
Evaluate the power
x2−16=1
Move the constant to the right-hand side and change its sign
x2=1+16
Add the numbers
x2=17
Take the root of both sides of the equation and remember to use both positive and negative roots
x=±17
Separate the equation into 2 possible cases
x=17x=−17
Check if the solution is in the defined range
x=17x=−17,x∈(−∞,−4)∪(4,+∞)
Find the intersection of the solution and the defined range
x=17x=−17
Solution
x1=−17,x2=17
Alternative Form
x1≈−4.123106,x2≈4.123106
Show Solution

Graph