Solve ln(x^2)=-2 - ScanMath

Evaluate

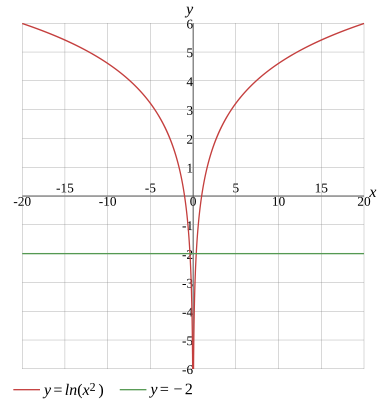
ln (x^{2}) = - 2

Find the domain

More Steps

ln (x^{2}) = - 2, x \neq = 0

Convert the logarithm into exponential form using the fact that lo g_{a} x = b is equal to x = a^{b}

x^{2} = e^{- 2}

Evaluate the power

x^{2} = \frac{1}{e ^{2}}

Take the root of both sides of the equation and remember to use both positive and negative roots

x = \pm \frac{1}{e ^{2}}

Simplify the expression

More Steps

x = \pm \frac{1}{e}

Separate the equation into 2 possible cases

x = \frac{1}{e} x = - \frac{1}{e}

Check if the solution is in the defined range

x = \frac{1}{e} x = - \frac{1}{e}, x \neq = 0

Find the intersection of the solution and the defined range

x = \frac{1}{e} x = - \frac{1}{e}

Solution

x_{1} = - \frac{1}{e}, x_{2} = \frac{1}{e}

Alternative Form

x_{1} \approx - 0.367879, x_{2} \approx 0.367879

Solve the equation