Question
Solve the equation
x=2
Evaluate
ln(x×2)=ln(x)×2
Find the domain
More Steps


Evaluate
{x×2>0x>0
Calculate
More Steps


Evaluate
x×2>0
Use the commutative property to reorder the terms
2x>0
Rewrite the expression
x>0
{x>0x>0
Find the intersection
x>0
ln(x×2)=ln(x)×2,x>0
Use the commutative property to reorder the terms
ln(2x)=ln(x)×2
Multiply the terms
ln(2x)=2ln(x)
Move the expression to the left side
ln(2x)−2ln(x)=0
Add the terms
More Steps


Evaluate
ln(2x)−2ln(x)
Use the logarithm base change rule
ln(2x)−ln(x2)
Use logax−logay=logayx to transform the expression
ln(x22x)
Reduce the fraction
More Steps


Calculate
x2x
Use the product rule aman=an−m to simplify the expression
x2−11
Subtract the terms
x11
Simplify
x1
ln(x2)
ln(x2)=0
Convert the logarithm into exponential form using the fact that logax=b is equal to x=ab
x2=e0
Evaluate the power
x2=1
Cross multiply
2=x
Swap the sides of the equation
x=2
Check if the solution is in the defined range
x=2,x>0
Solution
x=2
Show Solution

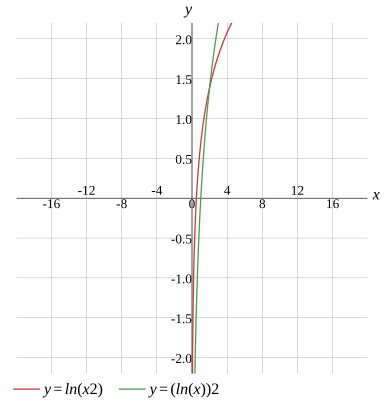
Graph