Solve log3(x-1)=2

Evaluate

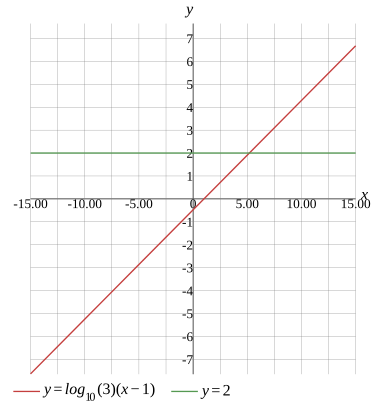
lo g_{10} (3) \times (x - 1) = 2

Divide both sides

\frac{lo g _{10} ( 3 ) \times ( x - 1 )}{lo g _{10} ( 3 )} = \frac{2}{lo g _{10} ( 3 )}

Divide the numbers

x - 1 = \frac{2}{lo g _{10} ( 3 )}

Move the constant to the right side

x = \frac{2}{lo g _{10} ( 3 )} + 1

Add the numbers

More Steps

x = lo g_{3} (300)

Solution

More Steps

x = 1 + 2 lo g_{3} (10)

Alternative Form

x \approx 5.191807

Solve the equation