Question
Solve the quadratic equation
Solve using square roots
Solve using the quadratic formula
Solve using the PQ formula
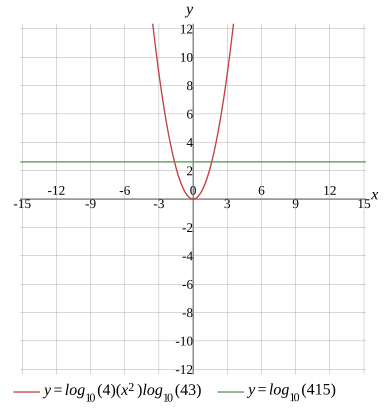
x1=−log10(43)2log2(415)×log10(43),x2=log10(43)2log2(415)×log10(43)
Alternative Form
x1≈−1.631599,x2≈1.631599
Evaluate
log10(4)×x2log10(43)=log10(415)
Multiply the numbers
log10(4)×log10(43)×x2=log10(415)
Divide both sides
log10(4)×log10(43)log10(4)×log10(43)×x2=log10(4)×log10(43)log10(415)
Divide the numbers
x2=log10(43)log4(415)
Take the root of both sides of the equation and remember to use both positive and negative roots
x=±log10(43)log4(415)
Simplify the expression
x=±log10(43)log4(415)×log10(43)
Separate the equation into 2 possible cases
x=log10(43)log4(415)×log10(43)x=−log10(43)log4(415)×log10(43)
Solve the equation
More Steps


Evaluate
x=log10(43)log4(415)×log10(43)
Simplify
More Steps


Evaluate
log10(43)log4(415)×log10(43)
Simplify
log10(43)21log2(415)×log10(43)
Expand the expression
log10(43)2log2(415)×log10(43)
x=log10(43)2log2(415)×log10(43)
x=log10(43)2log2(415)×log10(43)x=−log10(43)log4(415)×log10(43)
Solve the equation
More Steps


Evaluate
x=−log10(43)log4(415)×log10(43)
Simplify
More Steps


Evaluate
−log10(43)log4(415)×log10(43)
Simplify
−log10(43)21log2(415)×log10(43)
Expand the expression
−log10(43)2log2(415)×log10(43)
x=−log10(43)2log2(415)×log10(43)
x=log10(43)2log2(415)×log10(43)x=−log10(43)2log2(415)×log10(43)
Solution
x1=−log10(43)2log2(415)×log10(43),x2=log10(43)2log2(415)×log10(43)
Alternative Form
x1≈−1.631599,x2≈1.631599
Show Solution

Graph