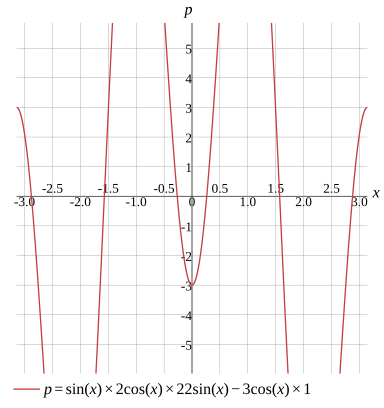
Solve p=sinx 2cosx 22sinx-3cosx 1

Evaluate

p = sin (x) \times 2 cos (x) \times 22 sin (x) - 3 cos (x) \times 1

Simplify

More Steps

p = 41 cos (x) - 44 cos^{3} (x)

Take the derivative of both sides

p^{'} = \frac{d}{d x} (41 cos (x) - 44 cos^{3} (x))

Use differentiation rule \frac{d}{d x} (f (x) \pm g (x)) = \frac{d}{d x} (f (x)) \pm \frac{d}{d x} (g (x))

p^{'} = \frac{d}{d x} (41 cos (x)) - \frac{d}{d x} (44 cos^{3} (x))

Calculate

More Steps

p^{'} = - 41 sin (x) - \frac{d}{d x} (44 cos^{3} (x))

Calculate

More Steps

p^{'} = - 41 sin (x) - (- 132 cos^{2} (x) sin (x))

Calculate

p^{'} = - 41 sin (x) + 132 cos^{2} (x) sin (x)

Solution

p^{'} = 25 sin (x) + 66 sin (x) cos (2 x)

Function