Question
Solve the equation
x∈R
Alternative Form
All real solution
Evaluate
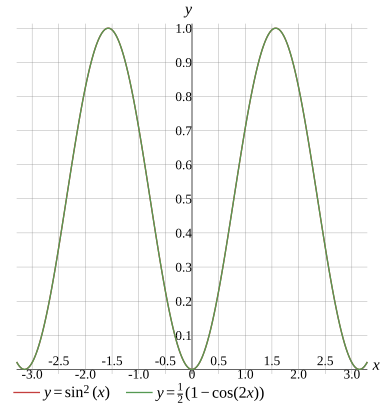
sin2(x)=21(1−cos(2x))
Multiply the terms
More Steps


Evaluate
21(1−cos(2x))
Use the the distributive property to expand the expression
21×1+21(−cos(2x))
Any expression multiplied by 1 remains the same
21+21(−cos(2x))
Rewrite the expression
21−21cos(2x)
sin2(x)=21−21cos(2x)
Use sin2(x)=1−cos2(x) to rewrite the expression
1−cos2(x)=21−21cos(2x)
Rewrite the expression
1−cos2(x)=21−21(2cos2(x)−1)
Expand the expression
1−cos2(x)=1−cos2(x)
Solution
x∈R
Alternative Form
All real solution
Show Solution

Verify the identity
true
Evaluate
sin2(x)=21(1−cos(2x))
Start working on the right-hand side
More Steps


Evaluate
21(1−cos(2x))
Use the the distributive property to expand the expression
21×1+21(−cos(2x))
Any expression multiplied by 1 remains the same
21+21(−cos(2x))
Rewrite the expression
21−21cos(2x)
Transform the expression
More Steps


Evaluate
−21cos(2x)
Use cos(2t)=cos2t−sin2t to transform the expression
−21(cos2(x)−sin2(x))
Use the the distributive property to expand the expression
−21cos2(x)−21(−sin2(x))
Multiply the terms
−21cos2(x)+21sin2(x)
21−21cos2(x)+21sin2(x)
Transform the expression
More Steps


Evaluate
−21cos2(x)
Use cos2t=1−sin2t to transform the expression
−21(1−sin2(x))
Use the the distributive property to expand the expression
−21×1−21(−sin2(x))
Any expression multiplied by 1 remains the same
−21−21(−sin2(x))
Multiply the terms
−21+21sin2(x)
21−21+21sin2(x)+21sin2(x)
Add the terms
More Steps


Evaluate
21sin2(x)+21sin2(x)
Collect like terms by calculating the sum or difference of their coefficients
(21+21)sin2(x)
Add the numbers
sin2(x)
21−21+sin2(x)
Since two opposites add up to 0,remove them form the expression
sin2(x)
sin2(x)=sin2(x)
Solution
true
Show Solution

Graph