Question
Solve the equation
a∈∅
Alternative Form
No solution
Evaluate
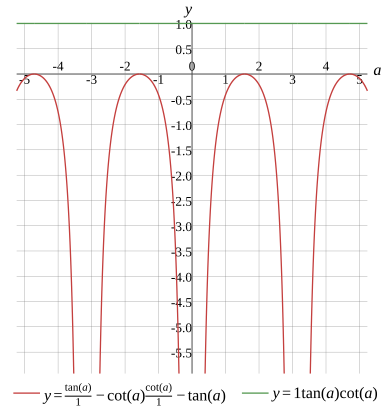
1tan(a)−cot(a)×1cot(a)−tan(a)=1×tan(a)cot(a)
Find the domain
More Steps


Evaluate
{a=2π+kπ,k∈Za=kπ,k∈Z
Find the intersection
a=2kπ,k∈Z
1tan(a)−cot(a)×1cot(a)−tan(a)=1×tan(a)cot(a),a=2kπ,k∈Z
Simplify
More Steps


Evaluate
1tan(a)−cot(a)×1cot(a)−tan(a)
Divide the terms
1tan(a)−cot(a)cot(a)−tan(a)
Divide the terms
tan(a)−cot(a)cot(a)−tan(a)
Multiply the terms
tan(a)−cot2(a)−tan(a)
The sum of two opposites equals 0
More Steps


Evaluate
tan(a)−tan(a)
Collect like terms
(1−1)tan(a)
Add the coefficients
0×tan(a)
Calculate
0
0−cot2(a)
Remove 0
−cot2(a)
−cot2(a)=1×tan(a)cot(a)
Multiply the terms
−cot2(a)=tan(a)cot(a)
Move the expression to the left side
−cot2(a)−tan(a)cot(a)=0
Factor the expression
More Steps


Calculate
−cot2(a)−tan(a)cot(a)
Factor out −1 from the expression
−(cot2(a)+tan(a)cot(a))
Factor the expression
More Steps


Calculate
cot2(a)+tan(a)cot(a)
Calculate
cot2(a)+cot(a)tan(a)
Rewrite the expression
cot(a)cot(a)+cot(a)tan(a)
Factor out cot(a) from the expression
cot(a)(cot(a)+tan(a))
−cot(a)(cot(a)+tan(a))
−cot(a)(cot(a)+tan(a))=0
Elimination the left coefficient
cot(a)(cot(a)+tan(a))=0
Separate the equation into 2 possible cases
cot(a)=0cot(a)+tan(a)=0
Solve the equation
More Steps


Evaluate
cot(a)=0
Use the inverse trigonometric function
a=arccot(0)
Calculate
a=2π
Add the period of kπ,k∈Z to find all solutions
a=2π+kπ,k∈Z
a=2π+kπ,k∈Zcot(a)+tan(a)=0
Solve the equation
More Steps


Evaluate
cot(a)+tan(a)=0
Rewrite the expression
sin(a)cos(a)+cos(a)sin(a)=0
Multiply both sides of the equation by LCD
(sin(a)cos(a)+cos(a)sin(a))sin(a)cos(a)=0×sin(a)cos(a)
Simplify the equation
More Steps


Evaluate
(sin(a)cos(a)+cos(a)sin(a))sin(a)cos(a)
Apply the distributive property
sin(a)cos(a)×sin(a)cos(a)+cos(a)sin(a)×sin(a)cos(a)
Simplify
cos(a)cos(a)+sin(a)sin(a)
Multiply the terms
cos2(a)+sin(a)sin(a)
Multiply the terms
cos2(a)+sin2(a)
cos2(a)+sin2(a)=0×sin(a)cos(a)
Any expression multiplied by 0 equals 0
cos2(a)+sin2(a)=0
Divide both sides
cos2(a)cos2(a)+cos2(a)sin2(a)=0
Divide the terms
1+cos2(a)sin2(a)=0
Rewrite the expression
1+tan2(a)=0
Since the left-hand side is always positive,and the right-hand side is always 0,the statement is false for any value of tan(a)
a∈/R
a=2π+kπ,k∈Za∈/R
Find the union
a=2π+kπ,k∈Z
Check if the solution is in the defined range
a=2π+kπ,k∈Z,a=2kπ,k∈Z
Solution
a∈∅
Alternative Form
No solution
Show Solution

Graph