Solve x = y^2 -6y 11

Identify the conic

Find the standard equation of the parabola

Find the vertex of the parabola

Find the focus of the parabola

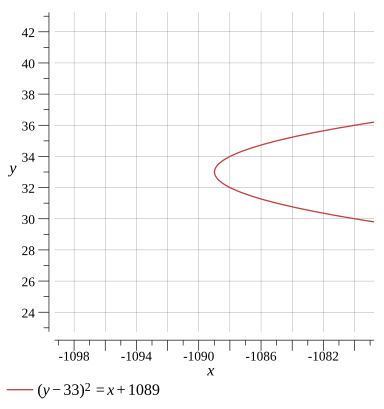
(y - 33)^{2} = x + 1089

Show Solution

Solve for x

Solve for y

x = y^{2} - 66 y

Show Solution

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Not symmetry with respect to the origin

Show Solution

Find the derivative with respect to x

Find the derivative with respect to y

\frac{d y}{d x} = \frac{1}{2 y - 66}

Show Solution

Find the second derivative with respect to x

Find the second derivative with respect to y

\frac{d ^{2} y}{d x ^{2}} = - \frac{1}{4 y ^{3} - 396 y ^{2} + 13068 y - 143748}

Calculate

x = y^{2} - 6 y 11

Simplify the expression

x = y^{2} - 66 y

Take the derivative of both sides

\frac{d}{d x} (x) = \frac{d}{d x} (y^{2} - 66 y)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

1 = \frac{d}{d x} (y^{2} - 66 y)

Calculate the derivative

More Steps

1 = 2 y \frac{d y}{d x} - 66 \frac{d y}{d x}

Swap the sides of the equation

2 y \frac{d y}{d x} - 66 \frac{d y}{d x} = 1

Collect like terms by calculating the sum or difference of their coefficients

(2 y - 66) \frac{d y}{d x} = 1

Divide both sides

\frac{( 2 y - 66 ) \frac{d y}{d x}}{2 y - 66} = \frac{1}{2 y - 66}

Divide the numbers

\frac{d y}{d x} = \frac{1}{2 y - 66}

Take the derivative of both sides

\frac{d}{d x} (\frac{d y}{d x}) = \frac{d}{d x} (\frac{1}{2 y - 66})

Calculate the derivative

\frac{d ^{2} y}{d x ^{2}} = \frac{d}{d x} (\frac{1}{2 y - 66})

Rewrite the expression in exponential form

\frac{d ^{2} y}{d x ^{2}} = \frac{d}{d x} ((2 y - 66)^{- 1})

Calculate the derivative

More Steps

\frac{d ^{2} y}{d x ^{2}} = - 2 \frac{d y}{d x} \times (2 y - 66)^{- 2}

Rewrite the expression

\frac{d ^{2} y}{d x ^{2}} = - \frac{2 \frac{d y}{d x}}{( 2 y - 66 ) ^{2}}

Calculate

\frac{d ^{2} y}{d x ^{2}} = - \frac{\frac{d y}{d x}}{2 ( y - 33 ) ^{2}}

Use equation \frac{d y}{d x} = \frac{1}{2 y - 66} to substitute

\frac{d ^{2} y}{d x ^{2}} = - \frac{\frac{1}{2 y - 66}}{2 ( y - 33 ) ^{2}}

Solution

More Steps

\frac{d ^{2} y}{d x ^{2}} = - \frac{1}{4 y ^{3} - 396 y ^{2} + 13068 y - 143748}

Show Solution

r = 0 r = \frac{cos ( θ ) + 66 sin ( θ )}{sin ^{2} ( θ )}

Show Solution