Solve x y=32x-y=3 - ScanMath

HOME CALCULATOR

DOWNLOAD FOR FREE

Algebra
Calculus
Trigonometry
Matrix

Type your math problem... x y=32x-y=3

Question

Solve the system of equations

(x_{1}, y_{1}) = (\frac{3 + 393}{64}, \frac{- 3 + 393}{2}) (x_{2}, y_{2}) = (\frac{3 - 393}{64}, - \frac{3 + 393}{2})

Evaluate

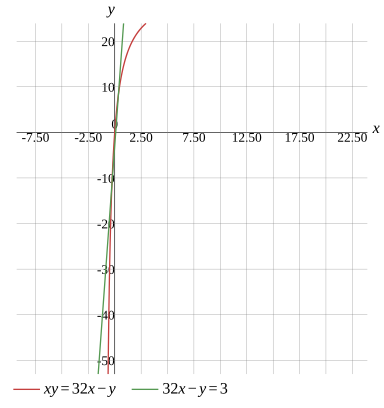
{x y = 32 x - y 32 x - y = 3

Solve the equation for y

More Steps

{x y = 32 x - y y = - 3 + 32 x

Substitute the given value of y into the equation x y = 32 x - y

x (- 3 + 32 x) = 32 x - (- 3 + 32 x)

Simplify

More Steps

x (- 3 + 32 x) = 3

Expand the expression

More Steps

- 3 x + 32 x^{2} = 3

Move the expression to the left side

- 3 x + 32 x^{2} - 3 = 0

Rewrite in standard form

32 x^{2} - 3 x - 3 = 0

Substitute a= 32,b= - 3 and c= - 3 into the quadratic formula x = \frac{- b \pm b ^{2} - 4 a c}{2 a}

x = \frac{3 \pm ( - 3 ) ^{2} - 4 \times 32 ( - 3 )}{2 \times 32}

Simplify the expression

x = \frac{3 \pm ( - 3 ) ^{2} - 4 \times 32 ( - 3 )}{64}

Simplify the expression

More Steps

x = \frac{3 \pm 393}{64}

Separate the equation into 2 possible cases

x = \frac{3 + 393}{64} x = \frac{3 - 393}{64}

Evaluate the logic

x = \frac{3 + 393}{64} \cup x = \frac{3 - 393}{64}

Rearrange the terms

{x = \frac{3 + 393}{64} y = - 3 + 32 x \cup {x = \frac{3 - 393}{64} y = - 3 + 32 x

Calculate

More Steps

{x = \frac{3 + 393}{64} y = \frac{- 3 + 393}{2} \cup {x = \frac{3 - 393}{64} y = - 3 + 32 x

Calculate

More Steps

{x = \frac{3 + 393}{64} y = \frac{- 3 + 393}{2} \cup {x = \frac{3 - 393}{64} y = - \frac{3 + 393}{2}

Check the solution

More Steps

{x = \frac{3 + 393}{64} y = \frac{- 3 + 393}{2} \cup {x = \frac{3 - 393}{64} y = - \frac{3 + 393}{2}

Check the solution

More Steps

{x = \frac{3 + 393}{64} y = \frac{- 3 + 393}{2} \cup {x = \frac{3 - 393}{64} y = - \frac{3 + 393}{2}

Solution

(x_{1}, y_{1}) = (\frac{3 + 393}{64}, \frac{- 3 + 393}{2}) (x_{2}, y_{2}) = (\frac{3 - 393}{64}, - \frac{3 + 393}{2})

Show Solution

Graph

Graph