Solve x y=8;-3x-2y=-12

Evaluate

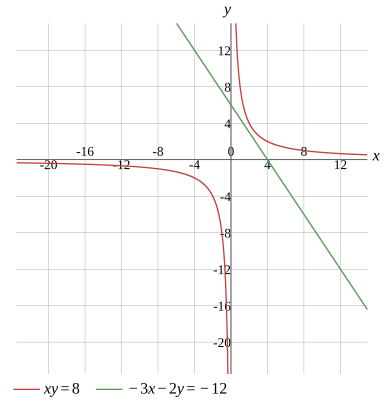
{x y = 8 - 3 x - 2 y = - 12

Solve the equation for x

More Steps

{x y = 8 x = \frac{12 - 2 y}{3}

Substitute the given value of x into the equation x y = 8

\frac{12 - 2 y}{3} \times y = 8

Simplify

More Steps

\frac{y ( 12 - 2 y )}{3} = 8

Cross multiply

y (12 - 2 y) = 3 \times 8

Simplify the equation

y (12 - 2 y) = 24

Expand the expression

More Steps

12 y - 2 y^{2} = 24

Move the expression to the left side

12 y - 2 y^{2} - 24 = 0

Rewrite in standard form

- 2 y^{2} + 12 y - 24 = 0

Multiply both sides

2 y^{2} - 12 y + 24 = 0

Substitute a= 2,b= - 12 and c= 24 into the quadratic formula y = \frac{- b \pm b ^{2} - 4 a c}{2 a}

y = \frac{12 \pm ( - 12 ) ^{2} - 4 \times 2 \times 24}{2 \times 2}

Simplify the expression

y = \frac{12 \pm ( - 12 ) ^{2} - 4 \times 2 \times 24}{4}

Simplify the expression

More Steps

y = \frac{12 \pm - 48}{4}

The expression is undefined in the set of real numbers

y \in / R

Solution

(x, y) \in / R^{2}

Alternative Form

No real solution

Solve the system of equations