Algebra
Calculus
Trigonometry
Matrix
Question
Solve the system of equations
Solve using the substitution method
Solve using the elimination method
Solve using the Gauss-Jordan method
Load more
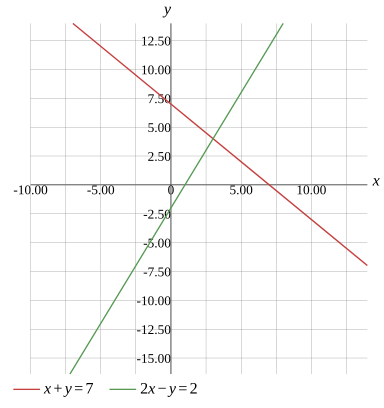
(x,y)=(3,4)
Evaluate
{x+y=72x−y=2
Solve the equation for x
{x=7−y2x−y=2
Substitute the given value of x into the equation 2x−y=2
2(7−y)−y=2
Simplify
More Steps
Evaluate
2(7−y)−y
Expand the expression
More Steps
Calculate
2(7−y)
Apply the distributive property
2×7−2y
Multiply the numbers
14−2y
14−2y−y
Subtract the terms
More Steps
Evaluate
−2y−y
Collect like terms by calculating the sum or difference of their coefficients
(−2−1)y
Subtract the numbers
−3y
14−3y
14−3y=2
Move the constant to the right-hand side and change its sign
−3y=2−14
Subtract the numbers
−3y=−12
Change the signs on both sides of the equation
3y=12
Divide both sides
33y=312
Divide the numbers
y=312
Divide the numbers
More Steps
Evaluate
312
Reduce the numbers
14
Calculate
4
y=4
Substitute the given value of y into the equation x=7−y
x=7−4
Calculate
x=3
Calculate
{x=3y=4
Check the solution
More Steps
Check the solution
{3+4=72×3−4=2
Simplify
{7=72=2
Evaluate
true
{x=3y=4
Solution
(x,y)=(3,4)
Show Solution
Relationship between lines
Neither parallel nor perpendicular
Evaluate
x+y=7,2x−y=2
Write the equation in slope-intercept form
More Steps
Evaluate
x+y=7
Move the expression to the right side
y=7−x
Rearrange the terms
y=−x+7
y=−x+7,2x−y=2
Write the equation in slope-intercept form
More Steps
Evaluate
2x−y=2
Move the expression to the right side
−y=2−2x
Divide both sides
y=−2+2x
Rearrange the terms
y=2x−2
y=−x+7,y=2x−2
Since the line is in slope-intercept form, the coefficient −1 is the slope of the line
−1,y=2x−2
Since the line is in slope-intercept form, the coefficient 2 is the slope of the line
−1,2
The slopes are different, so the lines aren't parallel. We'll multiply the slopes to check their relationship
−2
Solution
Neither parallel nor perpendicular
Show Solution
Graph
