Question
Solve the equation
x=−23
Alternative Form
x=−1.5
Evaluate
2x−23(2x−61)=4
Simplify
More Steps


Evaluate
2x−23(2x−61)
Multiply the terms
More Steps


Evaluate
23(2x−61)
Apply the distributive property
23×2x−23×61
Multiply the numbers
3x−23×61
Multiply the numbers
3x−41
2x−(3x−41)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
2x−3x+41
2x−3x+41=4
Multiply both sides of the equation by LCD
(2x−3x+41)×4=4×4
Simplify the equation
More Steps


Evaluate
(2x−3x+41)×4
Apply the distributive property
2x×4−3x×4+41×4
Simplify
x×2−3x×4+1
Use the commutative property to reorder the terms
2x−3x×4+1
Multiply the numbers
2x−12x+1
Subtract the terms
More Steps


Evaluate
2x−12x
Collect like terms by calculating the sum or difference of their coefficients
(2−12)x
Subtract the numbers
−10x
−10x+1
−10x+1=4×4
Simplify the equation
−10x+1=16
Move the constant to the right side
−10x=16−1
Subtract the numbers
−10x=15
Change the signs on both sides of the equation
10x=−15
Divide both sides
1010x=10−15
Divide the numbers
x=10−15
Solution
More Steps


Evaluate
10−15
Cancel out the common factor 5
2−3
Use b−a=−ba=−ba to rewrite the fraction
−23
x=−23
Alternative Form
x=−1.5
Show Solution

Rewrite the equation
2x=−3
Evaluate
2x−23(2x−61)=4
Evaluate
More Steps


Evaluate
2x−23(2x−61)
Multiply the terms
More Steps


Evaluate
23(2x−61)
Apply the distributive property
23×2x−23×61
Multiply the numbers
3x−23×61
Multiply the numbers
3x−41
2x−(3x−41)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
2x−3x+41
2x−3x+41=4
Rewrite the expression
21x−3x+41=4
Multiply both sides of the equation by LCD
−10x+1=16
Move the constant to the right side
−10x=15
Multiply both sides
10x=−15
Solution
2x=−3
Show Solution

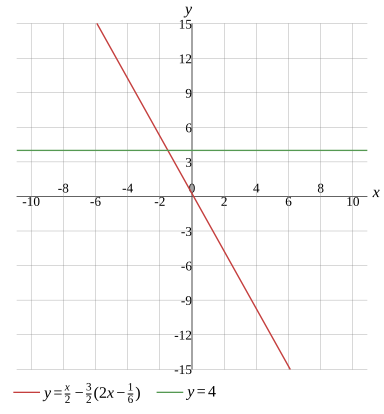
Graph