Solve x^2 + 2 y = 4

Question

Function

Find the x -intercept/zero

Find the y-intercept

x_{1} = - 2, x_{2} = 2

Evaluate

x^{2} + 2 y = 4

To find the x -intercept,set y =0

x^{2} + 2 \times 0 = 4

Any expression multiplied by 0 equals 0

x^{2} + 0 = 4

Removing 0 doesn't change the value,so remove it from the expression

x^{2} = 4

Take the root of both sides of the equation and remember to use both positive and negative roots

x = \pm 4

Simplify the expression

More Steps

Evaluate

4

Write the number in exponential form with the base of 2

2^{2}

Reduce the index of the radical and exponent with 2

2

x = \pm 2

Separate the equation into 2 possible cases

x = 2 x = - 2

Solution

x_{1} = - 2, x_{2} = 2

Show Solution

Solve the equation

Solve for x

Solve for y

x = 4 - 2 y x = - 4 - 2 y

Evaluate

x^{2} + 2 y = 4

Move the expression to the right-hand side and change its sign

x^{2} = 4 - 2 y

Take the root of both sides of the equation and remember to use both positive and negative roots

x = \pm 4 - 2 y

Solution

x = 4 - 2 y x = - 4 - 2 y

Show Solution

Testing for symmetry

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Not symmetry with respect to the origin

Evaluate

x^{2} + 2 y = 4

To test if the graph of x^{2} + 2 y = 4 is symmetry with respect to the origin,substitute -x for x and -y for y

(- x)^{2} + 2 (- y) = 4

Evaluate

More Steps

Evaluate

(- x)^{2} + 2 (- y)

Multiply the numbers

(- x)^{2} - 2 y

Rewrite the expression

x^{2} - 2 y

x^{2} - 2 y = 4

Solution

Not symmetry with respect to the origin

Show Solution

Identify the conic

Find the standard equation of the parabola

Find the vertex of the parabola

Find the focus of the parabola

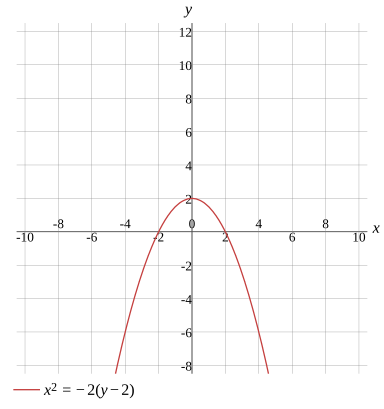
x^{2} = - 2 (y - 2)

Evaluate

x^{2} + 2 y = 4

Move the expression to the right-hand side and change its sign

x^{2} = 4 - 2 y

Use the commutative property to reorder the terms

x^{2} = - 2 y + 4

Solution

x^{2} = - 2 (y - 2)

Show Solution

Rewrite the equation

r = \frac{- sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )} r = - \frac{sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )}

Evaluate

x^{2} + 2 y = 4

To convert the equation to polar coordinates,substitute x for r cos (θ) and y for r sin (θ)

(cos (θ) \times r)^{2} + 2 sin (θ) \times r = 4

Factor the expression

cos^{2} (θ) \times r^{2} + 2 sin (θ) \times r = 4

Subtract the terms

cos^{2} (θ) \times r^{2} + 2 sin (θ) \times r - 4 = 4 - 4

Evaluate

cos^{2} (θ) \times r^{2} + 2 sin (θ) \times r - 4 = 0

Solve using the quadratic formula

r = \frac{- 2 sin ( θ ) \pm ( 2 sin ( θ ) ) ^{2} - 4 cos ^{2} ( θ ) ( - 4 )}{2 cos ^{2} ( θ )}

Simplify

r = \frac{- 2 sin ( θ ) \pm 4 + 12 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Separate the equation into 2 possible cases

r = \frac{- 2 sin ( θ ) + 4 + 12 cos ^{2} ( θ )}{2 cos ^{2} ( θ )} r = \frac{- 2 sin ( θ ) - 4 + 12 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Evaluate

More Steps

Evaluate

\frac{- 2 sin ( θ ) + 4 + 12 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Simplify the root

More Steps

Evaluate

4 + 12 cos^{2} (θ)

Factor the expression

4 (1 + 3 cos^{2} (θ))

Write the number in exponential form with the base of 2

2^{2} (1 + 3 cos^{2} (θ))

Calculate

2 1 + 3 cos^{2} (θ)

\frac{- 2 sin ( θ ) + 2 1 + 3 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Factor

\frac{2 ( - sin ( θ ) + 1 + 3 cos ^{2} ( θ ) )}{2 cos ^{2} ( θ )}

Reduce the fraction

\frac{- sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )}

r = \frac{- sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )} r = \frac{- 2 sin ( θ ) - 4 + 12 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Solution

More Steps

Evaluate

\frac{- 2 sin ( θ ) - 4 + 12 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Simplify the root

More Steps

Evaluate

4 + 12 cos^{2} (θ)

Factor the expression

4 (1 + 3 cos^{2} (θ))

Write the number in exponential form with the base of 2

2^{2} (1 + 3 cos^{2} (θ))

Calculate

2 1 + 3 cos^{2} (θ)

\frac{- 2 sin ( θ ) - 2 1 + 3 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Use \frac{- a}{b} = \frac{a}{- b} = - \frac{a}{b} to rewrite the fraction

- \frac{2 sin ( θ ) + 2 1 + 3 cos ^{2} ( θ )}{2 cos ^{2} ( θ )}

Factor

- \frac{2 ( sin ( θ ) + 1 + 3 cos ^{2} ( θ ) )}{2 cos ^{2} ( θ )}

Reduce the fraction

- \frac{sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )}

r = \frac{- sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )} r = - \frac{sin ( θ ) + 1 + 3 cos ^{2} ( θ )}{cos ^{2} ( θ )}

Show Solution

Find the first derivative

Find the derivative with respect to x

Find the derivative with respect to y

\frac{d y}{d x} = - x

Calculate

x^{2} + 2 y = 4

Take the derivative of both sides

\frac{d}{d x} (x^{2} + 2 y) = \frac{d}{d x} (4)

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (x^{2} + 2 y)

Use differentiation rules

\frac{d}{d x} (x^{2}) + \frac{d}{d x} (2 y)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

2 x + \frac{d}{d x} (2 y)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (2 y)

Use differentiation rules

\frac{d}{d y} (2 y) \times \frac{d y}{d x}

Evaluate the derivative

2 \frac{d y}{d x}

2 x + 2 \frac{d y}{d x}

2 x + 2 \frac{d y}{d x} = \frac{d}{d x} (4)

Calculate the derivative

2 x + 2 \frac{d y}{d x} = 0

Move the expression to the right-hand side and change its sign

2 \frac{d y}{d x} = 0 - 2 x

Removing 0 doesn't change the value,so remove it from the expression

2 \frac{d y}{d x} = - 2 x

Divide both sides

\frac{2 \frac{d y}{d x}}{2} = \frac{- 2 x}{2}

Divide the numbers

\frac{d y}{d x} = \frac{- 2 x}{2}

Solution

More Steps

Evaluate

\frac{- 2 x}{2}

Reduce the numbers

\frac{- x}{1}

Calculate

- x

\frac{d y}{d x} = - x

Show Solution

Find the second derivative

Find the second derivative with respect to x

Find the second derivative with respect to y

\frac{d ^{2} y}{d x ^{2}} = - 1

Calculate

x^{2} + 2 y = 4

Take the derivative of both sides

\frac{d}{d x} (x^{2} + 2 y) = \frac{d}{d x} (4)

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (x^{2} + 2 y)

Use differentiation rules

\frac{d}{d x} (x^{2}) + \frac{d}{d x} (2 y)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

2 x + \frac{d}{d x} (2 y)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (2 y)

Use differentiation rules

\frac{d}{d y} (2 y) \times \frac{d y}{d x}

Evaluate the derivative

2 \frac{d y}{d x}

2 x + 2 \frac{d y}{d x}

2 x + 2 \frac{d y}{d x} = \frac{d}{d x} (4)

Calculate the derivative

2 x + 2 \frac{d y}{d x} = 0

Move the expression to the right-hand side and change its sign

2 \frac{d y}{d x} = 0 - 2 x

Removing 0 doesn't change the value,so remove it from the expression

2 \frac{d y}{d x} = - 2 x

Divide both sides

\frac{2 \frac{d y}{d x}}{2} = \frac{- 2 x}{2}

Divide the numbers

\frac{d y}{d x} = \frac{- 2 x}{2}

Divide the numbers

More Steps

Evaluate

\frac{- 2 x}{2}

Reduce the numbers

\frac{- x}{1}

Calculate

- x

\frac{d y}{d x} = - x

Take the derivative of both sides

\frac{d}{d x} (\frac{d y}{d x}) = \frac{d}{d x} (- x)

Calculate the derivative

\frac{d ^{2} y}{d x ^{2}} = \frac{d}{d x} (- x)

Use differentiation rule \frac{d}{d x} (c f (x)) = c \times \frac{d}{d x} (f (x))

\frac{d ^{2} y}{d x ^{2}} = - \frac{d}{d x} (x)

Solution

\frac{d ^{2} y}{d x ^{2}} = - 1

Show Solution

Function

Solve the equation

Testing for symmetry

Identify the conic

Rewrite the equation

Find the first derivative

Find the second derivative

Graph