Solve x^2 + 4 y^2 - 24 x + 32 = 0

Question

Identify the conic

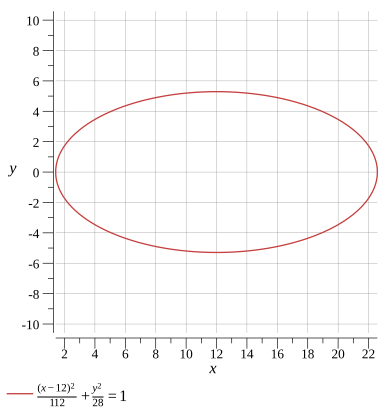
Find the standard equation of the ellipse

Find the center of the ellipse

Find the foci of the ellipse

\frac{( x - 12 ) ^{2}}{112} + \frac{y ^{2}}{28} = 1

Show Solution

Solve the equation

Solve for x

Solve for y

x = 12 + 2 28 - y^{2} x = 12 - 2 28 - y^{2}

Show Solution

Testing for symmetry

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Not symmetry with respect to the origin

Show Solution

Find the first derivative

Find the derivative with respect to x

Find the derivative with respect to y

\frac{d y}{d x} = \frac{- x + 12}{4 y}

Show Solution

Find the second derivative

Find the second derivative with respect to x

Find the second derivative with respect to y

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y ^{2} - x ^{2} + 24 x - 144}{16 y ^{3}}

Calculate

x^{2} + 4 y^{2} - 24 x + 32 = 0

Take the derivative of both sides

\frac{d}{d x} (x^{2} + 4 y^{2} - 24 x + 32) = \frac{d}{d x} (0)

Calculate the derivative

More Steps

2 x + 8 y \frac{d y}{d x} - 24 = \frac{d}{d x} (0)

Calculate the derivative

2 x + 8 y \frac{d y}{d x} - 24 = 0

Move the expression to the right-hand side and change its sign

8 y \frac{d y}{d x} = 0 - (2 x - 24)

Subtract the terms

More Steps

8 y \frac{d y}{d x} = - 2 x + 24

Divide both sides

\frac{8 y \frac{d y}{d x}}{8 y} = \frac{- 2 x + 24}{8 y}

Divide the numbers

\frac{d y}{d x} = \frac{- 2 x + 24}{8 y}

Divide the numbers

More Steps

\frac{d y}{d x} = \frac{- x + 12}{4 y}

Take the derivative of both sides

\frac{d}{d x} (\frac{d y}{d x}) = \frac{d}{d x} (\frac{- x + 12}{4 y})

Calculate the derivative

\frac{d ^{2} y}{d x ^{2}} = \frac{d}{d x} (\frac{- x + 12}{4 y})

Use differentiation rules

\frac{d ^{2} y}{d x ^{2}} = \frac{\frac{d}{d x} ( - x + 12 ) \times 4 y - ( - x + 12 ) \times \frac{d}{d x} ( 4 y )}{( 4 y ) ^{2}}

Calculate the derivative

More Steps

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y - ( - x + 12 ) \times \frac{d}{d x} ( 4 y )}{( 4 y ) ^{2}}

Calculate the derivative

More Steps

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y - ( - x + 12 ) \times 4 \frac{d y}{d x}}{( 4 y ) ^{2}}

Calculate

More Steps

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y - ( - 4 x \frac{d y}{d x} + 48 \frac{d y}{d x} )}{( 4 y ) ^{2}}

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y + 4 x \frac{d y}{d x} - 48 \frac{d y}{d x}}{( 4 y ) ^{2}}

Calculate

More Steps

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y + 4 x \frac{d y}{d x} - 48 \frac{d y}{d x}}{16 y ^{2}}

Calculate

\frac{d ^{2} y}{d x ^{2}} = \frac{- y + x \frac{d y}{d x} - 12 \frac{d y}{d x}}{4 y ^{2}}

Use equation \frac{d y}{d x} = \frac{- x + 12}{4 y} to substitute

\frac{d ^{2} y}{d x ^{2}} = \frac{- y + x \times \frac{- x + 12}{4 y} - 12 \times \frac{- x + 12}{4 y}}{4 y ^{2}}

Solution

More Steps

\frac{d ^{2} y}{d x ^{2}} = \frac{- 4 y ^{2} - x ^{2} + 24 x - 144}{16 y ^{3}}

Show Solution

Rewrite the equation

r = \frac{12 cos ( θ ) + 4 15 cos ^{2} ( θ ) - 8}{- 3 cos ^{2} ( θ ) + 4} r = \frac{12 cos ( θ ) - 4 15 cos ^{2} ( θ ) - 8}{- 3 cos ^{2} ( θ ) + 4}

Show Solution

Identify the conic

Solve the equation

Testing for symmetry

Find the first derivative

Find the second derivative

Rewrite the equation

Graph