Solve x^2+(y-3\sqrt x^2)2=1

Function

Find the x -intercept/zero

Find the y-intercept

x_{1} = 3 - 10, x_{2} = 3 + 10

Show Solution

Solve the equation

Solve for x

Solve for y

x = 3 + 10 - 2 y x = 3 - 10 - 2 y

Evaluate

x^{2} + (y - 3 (x)^{2}) \times 2 = 1

Simplify

More Steps

x^{2} + 2 (y - 3 x) = 1

Move the expression to the left side

x^{2} + 2 (y - 3 x) - 1 = 0

Calculate

More Steps

x^{2} + 2 y - 6 x - 1 = 0

Simplify

x^{2} + 2 y - 1 - 6 x = 0

Rewrite in standard form

x^{2} - 6 x + 2 y - 1 = 0

Substitute a= 1,b= - 6 and c= 2 y - 1 into the quadratic formula x = \frac{- b \pm b ^{2} - 4 a c}{2 a}

x = \frac{6 \pm ( - 6 ) ^{2} - 4 ( 2 y - 1 )}{2}

Simplify the expression

More Steps

x = \frac{6 \pm 40 - 8 y}{2}

Simplify the radical expression

More Steps

x = \frac{6 \pm 2 10 - 2 y}{2}

Separate the equation into 2 possible cases

x = \frac{6 + 2 10 - 2 y}{2} x = \frac{6 - 2 10 - 2 y}{2}

Simplify the expression

More Steps

x = 3 + 10 - 2 y x = \frac{6 - 2 10 - 2 y}{2}

Solution

More Steps

x = 3 + 10 - 2 y x = 3 - 10 - 2 y

Show Solution

Testing for symmetry

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Not symmetry with respect to the origin

Show Solution

Identify the conic

Find the standard equation of the parabola

Find the vertex of the parabola

Find the focus of the parabola

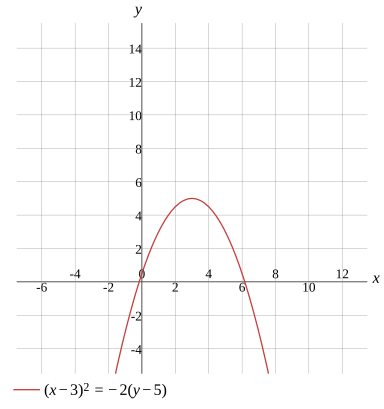
(x - 3)^{2} = - 2 (y - 5)

Show Solution

Rewrite the equation

r = \frac{- sin ( θ ) + 3 cos ( θ ) + 1 + 9 cos ^{2} ( θ ) - 3 sin ( 2 θ )}{cos ^{2} ( θ )} r = \frac{- sin ( θ ) + 3 cos ( θ ) - 1 + 9 cos ^{2} ( θ ) - 3 sin ( 2 θ )}{cos ^{2} ( θ )}

Evaluate

x^{2} + (y - 3 (x)^{2}) \times 2 = 1

Evaluate

More Steps

x^{2} + 2 y - 6 x = 1

To convert the equation to polar coordinates,substitute x for r cos (θ) and y for r sin (θ)

(cos (θ) \times r)^{2} + 2 sin (θ) \times r - 6 cos (θ) \times r = 1

Factor the expression

cos^{2} (θ) \times r^{2} + (2 sin (θ) - 6 cos (θ)) r = 1

Subtract the terms

cos^{2} (θ) \times r^{2} + (2 sin (θ) - 6 cos (θ)) r - 1 = 1 - 1

Evaluate

cos^{2} (θ) \times r^{2} + (2 sin (θ) - 6 cos (θ)) r - 1 = 0

Solve using the quadratic formula

r = \frac{- 2 sin ( θ ) + 6 cos ( θ ) \pm ( 2 sin ( θ ) - 6 cos ( θ ) ) ^{2} - 4 cos ^{2} ( θ ) ( - 1 )}{2 cos ^{2} ( θ )}

Simplify

r = \frac{- 2 sin ( θ ) + 6 cos ( θ ) \pm 4 + 36 cos ^{2} ( θ ) - 12 sin ( 2 θ )}{2 cos ^{2} ( θ )}

Separate the equation into 2 possible cases

r = \frac{- 2 sin ( θ ) + 6 cos ( θ ) + 4 + 36 cos ^{2} ( θ ) - 12 sin ( 2 θ )}{2 cos ^{2} ( θ )} r = \frac{- 2 sin ( θ ) + 6 cos ( θ ) - 4 + 36 cos ^{2} ( θ ) - 12 sin ( 2 θ )}{2 cos ^{2} ( θ )}

Evaluate

More Steps

r = \frac{- sin ( θ ) + 3 cos ( θ ) + 1 + 9 cos ^{2} ( θ ) - 3 sin ( 2 θ )}{cos ^{2} ( θ )} r = \frac{- 2 sin ( θ ) + 6 cos ( θ ) - 4 + 36 cos ^{2} ( θ ) - 12 sin ( 2 θ )}{2 cos ^{2} ( θ )}

Solution

More Steps

r = \frac{- sin ( θ ) + 3 cos ( θ ) + 1 + 9 cos ^{2} ( θ ) - 3 sin ( 2 θ )}{cos ^{2} ( θ )} r = \frac{- sin ( θ ) + 3 cos ( θ ) - 1 + 9 cos ^{2} ( θ ) - 3 sin ( 2 θ )}{cos ^{2} ( θ )}

Show Solution

Find the first derivative

Find the derivative with respect to x

Find the derivative with respect to y

\frac{d y}{d x} = - x + 3

Show Solution

Function

Solve the equation

Testing for symmetry

Identify the conic

Rewrite the equation

Find the first derivative

Graph