Question
Function
Find the x-intercept/zero
Find the y-intercept
x1=0,x2=1
Evaluate
x2−4y−x=0
To find the x-intercept,set y=0
x2−4×0−x=0
Any expression multiplied by 0 equals 0
x2−0−x=0
Removing 0 doesn't change the value,so remove it from the expression
x2−x=0
Factor the expression
More Steps


Evaluate
x2−x
Rewrite the expression
x×x−x
Factor out x from the expression
x(x−1)
x(x−1)=0
When the product of factors equals 0,at least one factor is 0
x=0x−1=0
Solve the equation for x
More Steps


Evaluate
x−1=0
Move the constant to the right-hand side and change its sign
x=0+1
Removing 0 doesn't change the value,so remove it from the expression
x=1
x=0x=1
Solution
x1=0,x2=1
Show Solution

Solve the equation
Solve for x
Solve for y
x=21+1+16yx=21−1+16y
Evaluate
x2−4y−x=0
Rewrite in standard form
x2−x−4y=0
Substitute a=1,b=−1 and c=−4y into the quadratic formula x=2a−b±b2−4ac
x=21±(−1)2−4(−4y)
Simplify the expression
More Steps


Evaluate
(−1)2−4(−4y)
Evaluate the power
1−4(−4y)
Multiply the numbers
More Steps


Evaluate
4(−4y)
Rewrite the expression
−4×4y
Multiply the terms
−16y
1−(−16y)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
1+16y
x=21±1+16y
Solution
x=21+1+16yx=21−1+16y
Show Solution

Testing for symmetry
Testing for symmetry about the origin
Testing for symmetry about the x-axis
Testing for symmetry about the y-axis
Not symmetry with respect to the origin
Evaluate
x2−4y−x=0
To test if the graph of x2−4y−x=0 is symmetry with respect to the origin,substitute -x for x and -y for y
(−x)2−4(−y)−(−x)=0
Evaluate
More Steps


Evaluate
(−x)2−4(−y)−(−x)
Multiply the numbers
(−x)2+4y−(−x)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
(−x)2+4y+x
Rewrite the expression
x2+4y+x
x2+4y+x=0
Solution
Not symmetry with respect to the origin
Show Solution

Identify the conic
Find the standard equation of the parabola
Find the vertex of the parabola
Find the focus of the parabola
Load more

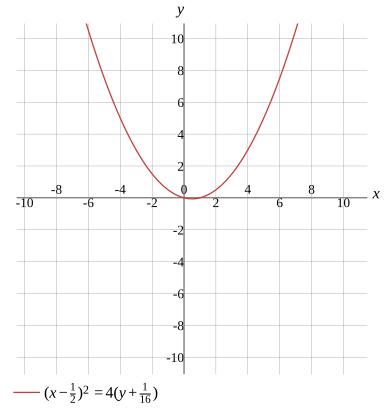
(x−21)2=4(y+161)
Evaluate
x2−4y−x=0
Move the expression to the right-hand side and change its sign
x2−x=0−(−4y)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
x2−x=0+4y
Removing 0 doesn't change the value,so remove it from the expression
x2−x=4y
To complete the square, the same value needs to be added to both sides
x2−x+41=4y+41
Use a2−2ab+b2=(a−b)2 to factor the expression
(x−21)2=4y+41
Solution
(x−21)2=4(y+161)
Show Solution

Rewrite the equation
r=0r=4sin(θ)sec2(θ)+sec(θ)
Evaluate
x2−4y−x=0
To convert the equation to polar coordinates,substitute x for rcos(θ) and y for rsin(θ)
(cos(θ)×r)2−4sin(θ)×r−cos(θ)×r=0
Factor the expression
cos2(θ)×r2+(−4sin(θ)−cos(θ))r=0
Factor the expression
r(cos2(θ)×r−4sin(θ)−cos(θ))=0
When the product of factors equals 0,at least one factor is 0
r=0cos2(θ)×r−4sin(θ)−cos(θ)=0
Solution
More Steps


Factor the expression
cos2(θ)×r−4sin(θ)−cos(θ)=0
Subtract the terms
cos2(θ)×r−4sin(θ)−cos(θ)−(−4sin(θ)−cos(θ))=0−(−4sin(θ)−cos(θ))
Evaluate
cos2(θ)×r=4sin(θ)+cos(θ)
Divide the terms
r=cos2(θ)4sin(θ)+cos(θ)
Simplify the expression
r=4sin(θ)sec2(θ)+sec(θ)
r=0r=4sin(θ)sec2(θ)+sec(θ)
Show Solution

Find the first derivative
Find the derivative with respect to x
Find the derivative with respect to y
dxdy=42x−1
Calculate
x2−4y−x=0
Take the derivative of both sides
dxd(x2−4y−x)=dxd(0)
Calculate the derivative
More Steps


Evaluate
dxd(x2−4y−x)
Use differentiation rules
dxd(x2)+dxd(−4y)+dxd(−x)
Use dxdxn=nxn−1 to find derivative
2x+dxd(−4y)+dxd(−x)
Evaluate the derivative
More Steps


Evaluate
dxd(−4y)
Use differentiation rules
dyd(−4y)×dxdy
Evaluate the derivative
−4dxdy
2x−4dxdy+dxd(−x)
Evaluate the derivative
More Steps


Evaluate
dxd(−x)
Use differentiation rule dxd(cf(x))=c×dxd(f(x))
−dxd(x)
Use dxdxn=nxn−1 to find derivative
−1
2x−4dxdy−1
2x−4dxdy−1=dxd(0)
Calculate the derivative
2x−4dxdy−1=0
Move the expression to the right-hand side and change its sign
−4dxdy=0−(2x−1)
Subtract the terms
More Steps


Evaluate
0−(2x−1)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
0−2x+1
Removing 0 doesn't change the value,so remove it from the expression
−2x+1
−4dxdy=−2x+1
Change the signs on both sides of the equation
4dxdy=2x−1
Divide both sides
44dxdy=42x−1
Solution
dxdy=42x−1
Show Solution

Find the second derivative
Find the second derivative with respect to x
Find the second derivative with respect to y
dx2d2y=21
Calculate
x2−4y−x=0
Take the derivative of both sides
dxd(x2−4y−x)=dxd(0)
Calculate the derivative
More Steps


Evaluate
dxd(x2−4y−x)
Use differentiation rules
dxd(x2)+dxd(−4y)+dxd(−x)
Use dxdxn=nxn−1 to find derivative
2x+dxd(−4y)+dxd(−x)
Evaluate the derivative
More Steps


Evaluate
dxd(−4y)
Use differentiation rules
dyd(−4y)×dxdy
Evaluate the derivative
−4dxdy
2x−4dxdy+dxd(−x)
Evaluate the derivative
More Steps


Evaluate
dxd(−x)
Use differentiation rule dxd(cf(x))=c×dxd(f(x))
−dxd(x)
Use dxdxn=nxn−1 to find derivative
−1
2x−4dxdy−1
2x−4dxdy−1=dxd(0)
Calculate the derivative
2x−4dxdy−1=0
Move the expression to the right-hand side and change its sign
−4dxdy=0−(2x−1)
Subtract the terms
More Steps


Evaluate
0−(2x−1)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
0−2x+1
Removing 0 doesn't change the value,so remove it from the expression
−2x+1
−4dxdy=−2x+1
Change the signs on both sides of the equation
4dxdy=2x−1
Divide both sides
44dxdy=42x−1
Divide the numbers
dxdy=42x−1
Take the derivative of both sides
dxd(dxdy)=dxd(42x−1)
Calculate the derivative
dx2d2y=dxd(42x−1)
Rewrite the expression
dx2d2y=4dxd(2x−1)
Evaluate the derivative
More Steps


Evaluate
dxd(2x−1)
Use differentiation rules
dxd(2x)+dxd(−1)
Evaluate the derivative
2+dxd(−1)
Use dxd(c)=0 to find derivative
2+0
Evaluate
2
dx2d2y=42
Solution
dx2d2y=21
Show Solution

Graph