Algebra
Calculus
Trigonometry
Matrix
Question
Solve the system of equations
(x1,y1)=(−0.468244,−58.443317)(x2,y2)=(0.495071,49.447967)
Evaluate
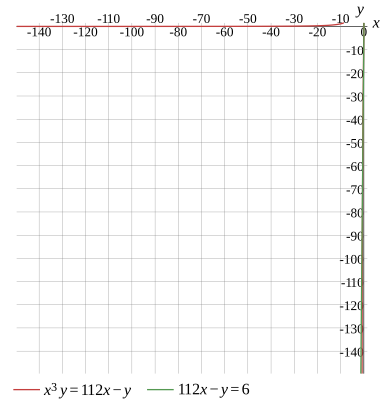
{x3y=112x−y112x−y=6
Solve the equation for y
More Steps
Evaluate
112x−y=6
Move the expression to the right-hand side and change its sign
−y=6−112x
Change the signs on both sides of the equation
y=−6+112x
{x3y=112x−yy=−6+112x
Substitute the given value of y into the equation x3y=112x−y
x3(−6+112x)=112x−(−6+112x)
Simplify
More Steps
Evaluate
112x−(−6+112x)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
112x+6−112x
The sum of two opposites equals 0
More Steps
Evaluate
112x−112x
Collect like terms
(112−112)x
Add the coefficients
0×x
Calculate
0
0+6
Remove 0
6
x3(−6+112x)=6
Expand the expression
More Steps
Evaluate
x3(−6+112x)
Apply the distributive property
x3(−6)+x3×112x
Use the commutative property to reorder the terms
−6x3+x3×112x
Multiply the terms
More Steps
Evaluate
x3×112x
Use the commutative property to reorder the terms
112x3×x
Multiply the terms
112x4
−6x3+112x4
−6x3+112x4=6
Move the expression to the left side
−6x3+112x4−6=0
Factor the expression
2(−3x3+56x4−3)=0
Divide both sides
−3x3+56x4−3=0
Calculate
x≈0.495071∪x≈−0.468244
Rearrange the terms
{x≈0.495071y=−6+112x∪{x≈−0.468244y=−6+112x
Calculate
More Steps
Evaluate
{x≈0.495071y=−6+112x
Substitute the given value of x into the equation y=−6+112x
y=−6+112×0.495071
Calculate
y≈49.447967
Calculate
{x≈0.495071y≈49.447967
{x≈0.495071y≈49.447967∪{x≈−0.468244y=−6+112x
Calculate
More Steps
Evaluate
{x≈−0.468244y=−6+112x
Substitute the given value of x into the equation y=−6+112x
y=−6+112(−0.468244)
Calculate
y≈−58.443317
Calculate
{x≈−0.468244y≈−58.443317
{x≈0.495071y≈49.447967∪{x≈−0.468244y≈−58.443317
Calculate
{x≈−0.468244y≈−58.443317∪{x≈0.495071y≈49.447967
Check the solution
{x≈−0.468244y≈−58.443317∪{x≈0.495071y≈49.447967
Solution
(x1,y1)=(−0.468244,−58.443317)(x2,y2)=(0.495071,49.447967)
Show Solution
Graph
