Question
Solve the equation
x1=−2log10(2)46(log10(2))3,x2=2log10(2)46(log10(2))3
Alternative Form
x1≈−1.056466,x2≈1.056466
Evaluate
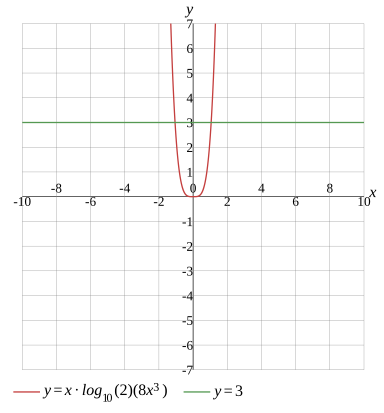
xlog10(2)×8x3=3
Multiply
More Steps


Evaluate
xlog10(2)×8x3
Multiply the terms with the same base by adding their exponents
x1+3log10(2)×8
Add the numbers
x4log10(2)×8
Use the commutative property to reorder the terms
log10(2)×x4×8
Use the commutative property to reorder the terms
8log10(2)×x4
8log10(2)×x4=3
Divide both sides
8log10(2)8log10(2)×x4=8log10(2)3
Divide the numbers
x4=8log10(2)3
Take the root of both sides of the equation and remember to use both positive and negative roots
x=±48log10(2)3
Simplify the expression
More Steps


Evaluate
48log10(2)3
To take a root of a fraction,take the root of the numerator and denominator separately
48log10(2)43
Multiply by the Conjugate
48log10(2)×483log10(2)43×483log10(2)
Simplify
48log10(2)×483log10(2)43×2242log10(2)
Multiply the numbers
More Steps


Evaluate
43×2242log10(2)
Multiply the terms
46log10(2)×22
Use the commutative property to reorder the terms
2246log10(2)
48log10(2)×483log10(2)2246log10(2)
Multiply the numbers
More Steps


Evaluate
48log10(2)×483log10(2)
The product of roots with the same index is equal to the root of the product
48log10(2)×83log10(2)
Calculate the product
4(64log10(2))2
Evaluate the root
64log10(2)
64log10(2)2246log10(2)
x=±64log10(2)2246log10(2)
Separate the equation into 2 possible cases
x=64log10(2)2246log10(2)x=−64log10(2)2246log10(2)
Calculate
More Steps


Evaluate
64log10(2)2246log10(2)
Multiply by the Conjugate
64log10(2)×64log10(2)2246log10(2)×64log10(2)
Calculate
64log10(2)2246log10(2)×64log10(2)
Calculate
More Steps


Evaluate
46log10(2)×64log10(2)
Use na=mnam to expand the expression
46log10(2)×4(64log10(2))2
The product of roots with the same index is equal to the root of the product
46log10(2)×(64log10(2))2
Calculate the product
46(64log10(2))2×log10(2)
64log10(2)2246(64log10(2))2×log10(2)
Reduce the fraction
24log10(2)46(64log10(2))2×log10(2)
x=24log10(2)46(64log10(2))2×log10(2)x=−64log10(2)2246log10(2)
Calculate
More Steps


Evaluate
−64log10(2)2246log10(2)
Evaluate
64log10(2)−2246log10(2)
Multiply by the Conjugate
64log10(2)×64log10(2)−2246log10(2)×64log10(2)
Calculate
64log10(2)−2246log10(2)×64log10(2)
Calculate
More Steps


Evaluate
46log10(2)×64log10(2)
Use na=mnam to expand the expression
46log10(2)×4(64log10(2))2
The product of roots with the same index is equal to the root of the product
46log10(2)×(64log10(2))2
Calculate the product
46(64log10(2))2×log10(2)
64log10(2)−2246(64log10(2))2×log10(2)
Simplify
−64log10(2)2246(64log10(2))2×log10(2)
Reduce the fraction
−24log10(2)46(64log10(2))2×log10(2)
x=24log10(2)46(64log10(2))2×log10(2)x=−24log10(2)46(64log10(2))2×log10(2)
Calculate
More Steps


Evaluate
24log10(2)46(64log10(2))2×log10(2)
Evaluate the power
More Steps


Evaluate
6(64log10(2))2×log10(2)
Evaluate the power
6×4096(log10(2))2×log10(2)
Multiply the terms
24576(log10(2))2×log10(2)
Multiply the terms
24576(log10(2))3
24log10(2)424576(log10(2))3
Evaluate the power
16log10(2)424576(log10(2))3
Rewrite the expression
More Steps


Evaluate
424576(log10(2))3
Rewrite the expression
424576×4(log10(2))3
Simplify the root
846(log10(2))3
16log10(2)846(log10(2))3
Reduce the fraction
2log10(2)46(log10(2))3
x=2log10(2)46(log10(2))3x=−24log10(2)46(64log10(2))2×log10(2)
Calculate
More Steps


Evaluate
−24log10(2)46(64log10(2))2×log10(2)
Evaluate the power
More Steps


Evaluate
6(64log10(2))2×log10(2)
Evaluate the power
6×4096(log10(2))2×log10(2)
Multiply the terms
24576(log10(2))2×log10(2)
Multiply the terms
24576(log10(2))3
−24log10(2)424576(log10(2))3
Evaluate the power
−16log10(2)424576(log10(2))3
Rewrite the expression
More Steps


Evaluate
424576(log10(2))3
Rewrite the expression
424576×4(log10(2))3
Simplify the root
846(log10(2))3
−16log10(2)846(log10(2))3
Reduce the fraction
−2log10(2)46(log10(2))3
x=2log10(2)46(log10(2))3x=−2log10(2)46(log10(2))3
Solution
x1=−2log10(2)46(log10(2))3,x2=2log10(2)46(log10(2))3
Alternative Form
x1≈−1.056466,x2≈1.056466
Show Solution

Graph