Solve y = x^24x^5

Question

Function

Find the inverse

Evaluate the derivative

Find the domain

f^{- 1} (x) = \frac{7 32 x}{2}

Evaluate

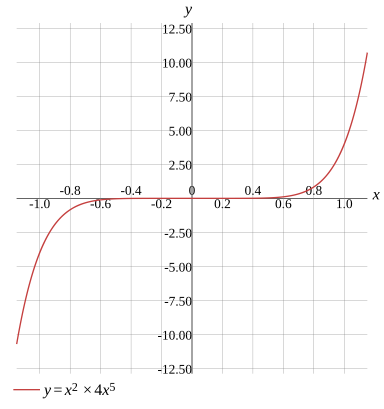
y = x^{2} \times 4 x^{5}

Simplify

More Steps

Evaluate

x^{2} \times 4 x^{5}

Multiply the terms with the same base by adding their exponents

x^{2 + 5} \times 4

Add the numbers

x^{7} \times 4

Use the commutative property to reorder the terms

4 x^{7}

y = 4 x^{7}

Interchange x and y

x = 4 y^{7}

Swap the sides of the equation

4 y^{7} = x

Divide both sides

\frac{4 y ^{7}}{4} = \frac{x}{4}

Divide the numbers

y^{7} = \frac{x}{4}

Take the 7 -th root on both sides of the equation

7 y^{7} = 7 \frac{x}{4}

Calculate

y = 7 \frac{x}{4}

Simplify the root

More Steps

Evaluate

7 \frac{x}{4}

To take a root of a fraction,take the root of the numerator and denominator separately

\frac{7 x}{7 4}

Multiply by the Conjugate

\frac{7 x \times 7 4 ^{6}}{7 4 \times 7 4 ^{6}}

Calculate

\frac{7 x \times 7 4 ^{6}}{2 ^{2}}

Calculate

More Steps

Evaluate

7 x \times 7 4^{6}

The product of roots with the same index is equal to the root of the product

7 x \times 4^{6}

Calculate the product

7 4^{6} x

Rewrite the exponent as a sum

7 2^{7 + 5} x

Use a^{m + n} = a^{m} \times a^{n} to expand the expression

7 2^{7} \times 2^{5} x

The root of a product is equal to the product of the roots of each factor

7 2^{7} \times 7 2^{5} x

Reduce the index of the radical and exponent with 7

2 7 32 x

\frac{2 7 32 x}{2 ^{2}}

Reduce the fraction

More Steps

Evaluate

\frac{2}{2 ^{2}}

Use the product rule \frac{a ^{n}}{a ^{m}} = a^{n - m} to simplify the expression

\frac{1}{2 ^{2 - 1}}

Subtract the terms

\frac{1}{2 ^{1}}

Simplify

\frac{1}{2}

\frac{7 32 x}{2}

y = \frac{7 32 x}{2}

Solution

f^{- 1} (x) = \frac{7 32 x}{2}

Show Solution

Testing for symmetry

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Symmetry with respect to the origin

Evaluate

y = x^{2} 4 x^{5}

Simplify the expression

y = 4 x^{7}

To test if the graph of y = 4 x^{7} is symmetry with respect to the origin,substitute -x for x and -y for y

- y = 4 (- x)^{7}

Simplify

More Steps

Evaluate

4 (- x)^{7}

Rewrite the expression

4 (- x^{7})

Multiply the numbers

- 4 x^{7}

- y = - 4 x^{7}

Change the signs both sides

y = 4 x^{7}

Solution

Symmetry with respect to the origin

Show Solution

Solve the equation

Solve for x

Solve for y

x = \frac{7 32 y}{2}

Evaluate

y = x^{2} \times 4 x^{5}

Simplify

More Steps

Evaluate

x^{2} \times 4 x^{5}

Multiply the terms with the same base by adding their exponents

x^{2 + 5} \times 4

Add the numbers

x^{7} \times 4

Use the commutative property to reorder the terms

4 x^{7}

y = 4 x^{7}

Swap the sides of the equation

4 x^{7} = y

Divide both sides

\frac{4 x ^{7}}{4} = \frac{y}{4}

Divide the numbers

x^{7} = \frac{y}{4}

Take the 7 -th root on both sides of the equation

7 x^{7} = 7 \frac{y}{4}

Calculate

x = 7 \frac{y}{4}

Solution

More Steps

Evaluate

7 \frac{y}{4}

To take a root of a fraction,take the root of the numerator and denominator separately

\frac{7 y}{7 4}

Multiply by the Conjugate

\frac{7 y \times 7 4 ^{6}}{7 4 \times 7 4 ^{6}}

Calculate

\frac{7 y \times 7 4 ^{6}}{2 ^{2}}

Calculate

More Steps

Evaluate

7 y \times 7 4^{6}

The product of roots with the same index is equal to the root of the product

7 y \times 4^{6}

Calculate the product

7 4^{6} y

Rewrite the exponent as a sum

7 2^{7 + 5} y

Use a^{m + n} = a^{m} \times a^{n} to expand the expression

7 2^{7} \times 2^{5} y

The root of a product is equal to the product of the roots of each factor

7 2^{7} \times 7 2^{5} y

Reduce the index of the radical and exponent with 7

2 7 32 y

\frac{2 7 32 y}{2 ^{2}}

Reduce the fraction

More Steps

Evaluate

\frac{2}{2 ^{2}}

Use the product rule \frac{a ^{n}}{a ^{m}} = a^{n - m} to simplify the expression

\frac{1}{2 ^{2 - 1}}

Subtract the terms

\frac{1}{2 ^{1}}

Simplify

\frac{1}{2}

\frac{7 32 y}{2}

x = \frac{7 32 y}{2}

Show Solution

Rewrite the equation

r = 0 r = 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )} r = - 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )}

Evaluate

y = x^{2} \times 4 x^{5}

Simplify

More Steps

Evaluate

x^{2} \times 4 x^{5}

Multiply the terms with the same base by adding their exponents

x^{2 + 5} \times 4

Add the numbers

x^{7} \times 4

Use the commutative property to reorder the terms

4 x^{7}

y = 4 x^{7}

Move the expression to the left side

y - 4 x^{7} = 0

To convert the equation to polar coordinates,substitute x for r cos (θ) and y for r sin (θ)

sin (θ) \times r - 4 (cos (θ) \times r)^{7} = 0

Factor the expression

- 4 cos^{7} (θ) \times r^{7} + sin (θ) \times r = 0

Factor the expression

r (- 4 cos^{7} (θ) \times r^{6} + sin (θ)) = 0

When the product of factors equals 0,at least one factor is 0

r = 0 - 4 cos^{7} (θ) \times r^{6} + sin (θ) = 0

Solution

More Steps

Factor the expression

- 4 cos^{7} (θ) \times r^{6} + sin (θ) = 0

Subtract the terms

- 4 cos^{7} (θ) \times r^{6} + sin (θ) - sin (θ) = 0 - sin (θ)

Evaluate

- 4 cos^{7} (θ) \times r^{6} = - sin (θ)

Divide the terms

r^{6} = \frac{sin ( θ )}{4 cos ^{7} ( θ )}

Evaluate the power

r = \pm 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )}

Separate into possible cases

r = 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )} r = - 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )}

r = 0 r = 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )} r = - 6 \frac{sin ( θ )}{4 cos ^{7} ( θ )}

Show Solution

Function

Testing for symmetry

Solve the equation

Rewrite the equation

Graph