Question
Function
Evaluate the derivative
Find the domain
Find the x-intercept/zero
Load more

y′={2x+1,x<12x−1,x>1
Evaluate
y=x2−∣x−1∣
When the expression in absolute value bars is not negative, remove the bars
y=x2−∣x−1∣
Take the derivative of both sides
y′=dxd(x2−∣x−1∣)
Solution
y′={2x+1,x<12x−1,x>1
Show Solution

Testing for symmetry
Testing for symmetry about the origin
Testing for symmetry about the x-axis
Testing for symmetry about the y-axis
Not symmetry with respect to the origin
Evaluate
y=x2−∣x−1∣
Simplify the expression
y=x2−∣x−1∣
To test if the graph of y=x2−∣x−1∣ is symmetry with respect to the origin,substitute -x for x and -y for y
−y=(−x)2−∣−x−1∣
Simplify
More Steps


Evaluate
(−x)2−∣−x−1∣
Calculate the absolute value
(−x)2−∣x+1∣
Rewrite the expression
x2−∣x+1∣
−y=x2−∣x+1∣
Change the signs both sides
y=−x2+∣x+1∣
Solution
Not symmetry with respect to the origin
Show Solution

Solve the equation
Solve for x
Solve for y
x∈(−∞,1)∩x=−21+5+4y∪x∈(−∞,1)∩x=2−1+5+4y∪x∈[1,+∞)∩x=21+−3+4y∪x∈[1,+∞)∩x=21−−3+4y
Evaluate
y=x2−∣x−1∣
When the expression in absolute value bars is not negative, remove the bars
y=x2−∣x−1∣
Swap the sides of the equation
x2−∣x−1∣=y
Move the expression to the left side
x2−∣x−1∣−y=0
Separate the equation into 2 possible cases
x2−(x−1)−y=0,x−1≥0x2−(−(x−1))−y=0,x−1<0
Solve the equation
More Steps


Evaluate
x2−(x−1)−y=0
Calculate
x2−x+1−y=0
Substitute a=1,b=−1 and c=1−y into the quadratic formula x=2a−b±b2−4ac
x=21±(−1)2−4(1−y)
Simplify the expression
More Steps


Evaluate
(−1)2−4(1−y)
Evaluate the power
1−4(1−y)
Apply the distributive property
1−(4−4y)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
1−4+4y
Subtract the numbers
−3+4y
x=21±−3+4y
Separate the equation into 2 possible cases
x=21+−3+4yx=21−−3+4y
x=21+−3+4yx=21−−3+4y,x−1≥0x2−(−(x−1))−y=0,x−1<0
Solve the inequality
More Steps


Evaluate
x−1≥0
Move the constant to the right side
x≥0+1
Removing 0 doesn't change the value,so remove it from the expression
x≥1
x=21+−3+4yx=21−−3+4y,x≥1x2−(−(x−1))−y=0,x−1<0
Solve the equation
More Steps


Evaluate
x2−(−(x−1))−y=0
Calculate
x2+x−1−y=0
Substitute a=1,b=1 and c=−1−y into the quadratic formula x=2a−b±b2−4ac
x=2−1±12−4(−1−y)
Simplify the expression
More Steps


Evaluate
12−4(−1−y)
1 raised to any power equals to 1
1−4(−1−y)
Apply the distributive property
1−(−4−4y)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
1+4+4y
Add the numbers
5+4y
x=2−1±5+4y
Separate the equation into 2 possible cases
x=2−1+5+4yx=2−1−5+4y
Use b−a=−ba=−ba to rewrite the fraction
x=2−1+5+4yx=−21+5+4y
x=21+−3+4yx=21−−3+4y,x≥1x=2−1+5+4yx=−21+5+4y,x−1<0
Solve the inequality
More Steps


Evaluate
x−1<0
Move the constant to the right side
x<0+1
Removing 0 doesn't change the value,so remove it from the expression
x<1
x=21+−3+4yx=21−−3+4y,x≥1x=2−1+5+4yx=−21+5+4y,x<1
Find the intersection
x∈[1,+∞)∩x=21+−3+4y∪x∈[1,+∞)∩x=21−−3+4yx=2−1+5+4yx=−21+5+4y,x<1
Find the intersection
x∈[1,+∞)∩x=21+−3+4y∪x∈[1,+∞)∩x=21−−3+4yx∈(−∞,1)∩x=−21+5+4y∪x∈(−∞,1)∩x=2−1+5+4y
Solution
x∈(−∞,1)∩x=−21+5+4y∪x∈(−∞,1)∩x=2−1+5+4y∪x∈[1,+∞)∩x=21+−3+4y∪x∈[1,+∞)∩x=21−−3+4y
Show Solution

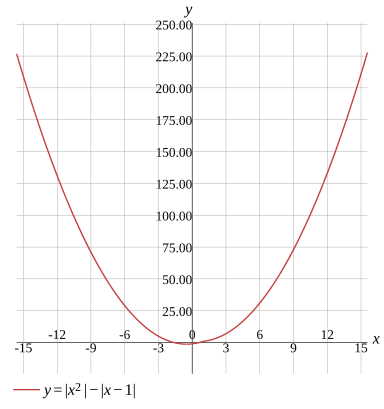
Graph