Question
Function
Evaluate the derivative
Find the domain
Find the x-intercept/zero
Load more

y′={x21,x<0−x21,x>0
Evaluate
y=x2×1∣x∣
Any expression multiplied by 1 remains the same
y=x2∣x∣
Take the derivative of both sides
y′=dxd(x2∣x∣)
Solution
y′={x21,x<0−x21,x>0
Show Solution

Testing for symmetry
Testing for symmetry about the origin
Testing for symmetry about the x-axis
Testing for symmetry about the y-axis
Not symmetry with respect to the origin
Evaluate
y=x21∣x∣
Simplify the expression
y=x2∣x∣
To test if the graph of y=x2∣x∣ is symmetry with respect to the origin,substitute -x for x and -y for y
−y=(−x)2∣−x∣
Simplify
More Steps


Evaluate
(−x)2∣−x∣
Calculate the absolute value
(−x)2∣x∣
Determine the sign
x2∣x∣
Rewrite the expression
∣x∣1
−y=∣x∣1
Change the signs both sides
y=−∣x∣1
Solution
Not symmetry with respect to the origin
Show Solution

Solve the equation
Solve for x
Solve for y
x=0x∈(−∞,0)∩x=−y1x∈[0,+∞)∩x=y1
Evaluate
y=x2×1∣x∣
Any expression multiplied by 1 remains the same
y=x2∣x∣
Swap the sides of the equation
x2∣x∣=y
Cross multiply
∣x∣=x2y
Simplify the equation
∣x∣=yx2
Rewrite the expression
∣x∣−yx2=0
Separate the equation into 2 possible cases
x−yx2=0,x≥0−x−yx2=0,x<0
Solve the equation
More Steps


Evaluate
x−yx2=0
Factor the expression
More Steps


Evaluate
x−yx2
Rewrite the expression
x−xyx
Factor out x from the expression
x(1−yx)
x(1−yx)=0
When the product of factors equals 0,at least one factor is 0
x=01−yx=0
Solve the equation for x
More Steps


Evaluate
1−yx=0
Move the constant to the right-hand side and change its sign
−yx=0−1
Removing 0 doesn't change the value,so remove it from the expression
−yx=−1
Divide both sides
−y−yx=−y−1
Divide the numbers
x=−y−1
Divide the numbers
x=y1
x=0x=y1
x=0x=y1,x≥0−x−yx2=0,x<0
Solve the equation
More Steps


Evaluate
−x−yx2=0
Factor the expression
More Steps


Evaluate
−x−yx2
Rewrite the expression
−x−xyx
Factor out −x from the expression
−x(1+yx)
−x(1+yx)=0
When the product of factors equals 0,at least one factor is 0
−x=01+yx=0
Solve the equation for x
x=01+yx=0
Solve the equation for x
More Steps


Evaluate
1+yx=0
Move the constant to the right-hand side and change its sign
yx=0−1
Removing 0 doesn't change the value,so remove it from the expression
yx=−1
Divide both sides
yyx=y−1
Divide the numbers
x=y−1
Use b−a=−ba=−ba to rewrite the fraction
x=−y1
x=0x=−y1
x=0x=y1,x≥0x=0x=−y1,x<0
Find the intersection
x=0x∈[0,+∞)∩x=y1x=0x=−y1,x<0
Find the intersection
x=0x∈[0,+∞)∩x=y1x∈(−∞,0)∩x=−y1
Solution
x=0x∈(−∞,0)∩x=−y1x∈[0,+∞)∩x=y1
Show Solution

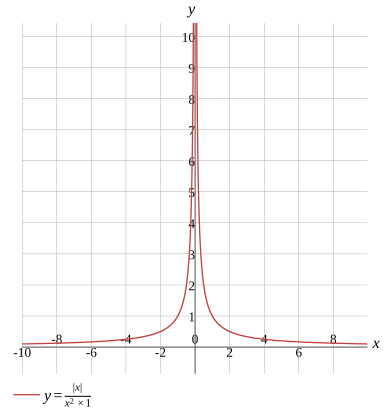
Graph