Question
Function
Find the vertex
Find the axis of symmetry
Rewrite in vertex form
Load more

(2,−2)
Evaluate
y=2(x−3)(x−1)
Write the quadratic function in standard form
y=2x2−8x+6
Find the x-coordinate of the vertex by substituting a=2 and b=−8 into x = −2ab
x=−2×2−8
Solve the equation for x
x=2
Find the y-coordinate of the vertex by evaluating the function for x=2
y=2×22−8×2+6
Calculate
More Steps


Evaluate
2×22−8×2+6
Calculate the product
23−8×2+6
Multiply the numbers
23−16+6
Evaluate the power
8−16+6
Calculate the sum or difference
−2
y=−2
Solution
(2,−2)
Show Solution

Testing for symmetry
Testing for symmetry about the origin
Testing for symmetry about the x-axis
Testing for symmetry about the y-axis
Not symmetry with respect to the origin
Evaluate
y=2(x−3)(x−1)
To test if the graph of y=2(x−3)(x−1) is symmetry with respect to the origin,substitute -x for x and -y for y
−y=2(−x−3)(−x−1)
Change the signs both sides
y=−2(−x−3)(−x−1)
Solution
Not symmetry with respect to the origin
Show Solution

Identify the conic
Find the standard equation of the parabola
Find the vertex of the parabola
Find the focus of the parabola
Load more

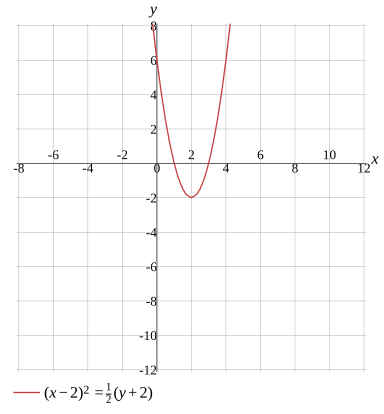
(x−2)2=21(y+2)
Evaluate
y=2(x−3)(x−1)
Calculate
y=2x2−8x+6
Swap the sides of the equation
2x2−8x+6=y
Move the constant to the right-hand side and change its sign
2x2−8x=y−6
Multiply both sides of the equation by 21
(2x2−8x)×21=(y−6)×21
Multiply the terms
More Steps


Evaluate
(2x2−8x)×21
Use the the distributive property to expand the expression
2x2×21−8x×21
Multiply the numbers
x2−8x×21
Multiply the numbers
x2−4x
x2−4x=(y−6)×21
Multiply the terms
More Steps


Evaluate
(y−6)×21
Apply the distributive property
y×21−6×21
Use the commutative property to reorder the terms
21y−6×21
Multiply the numbers
21y−3
x2−4x=21y−3
To complete the square, the same value needs to be added to both sides
x2−4x+4=21y−3+4
Use a2−2ab+b2=(a−b)2 to factor the expression
(x−2)2=21y−3+4
Add the numbers
(x−2)2=21y+1
Solution
(x−2)2=21(y+2)
Show Solution

Solve the equation
Solve for x
Solve for y
x=24+4+2yx=24−4+2y
Evaluate
y=2(x−3)(x−1)
Swap the sides of the equation
2(x−3)(x−1)=y
Expand the expression
More Steps


Evaluate
2(x−3)(x−1)
Multiply the terms
More Steps


Evaluate
2(x−3)
Apply the distributive property
2x−2×3
Multiply the numbers
2x−6
(2x−6)(x−1)
Apply the distributive property
2x×x−2x×1−6x−(−6×1)
Multiply the terms
2x2−2x×1−6x−(−6×1)
Any expression multiplied by 1 remains the same
2x2−2x−6x−(−6×1)
Any expression multiplied by 1 remains the same
2x2−2x−6x−(−6)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
2x2−2x−6x+6
Subtract the terms
More Steps


Evaluate
−2x−6x
Collect like terms by calculating the sum or difference of their coefficients
(−2−6)x
Subtract the numbers
−8x
2x2−8x+6
2x2−8x+6=y
Move the expression to the left side
2x2−8x+6−y=0
Substitute a=2,b=−8 and c=6−y into the quadratic formula x=2a−b±b2−4ac
x=2×28±(−8)2−4×2(6−y)
Simplify the expression
x=48±(−8)2−4×2(6−y)
Simplify the expression
More Steps


Evaluate
(−8)2−4×2(6−y)
Multiply the terms
More Steps


Multiply the terms
4×2(6−y)
Multiply the terms
8(6−y)
Apply the distributive property
8×6−8y
Multiply the numbers
48−8y
(−8)2−(48−8y)
Rewrite the expression
82−(48−8y)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
82−48+8y
Evaluate the power
64−48+8y
Subtract the numbers
16+8y
x=48±16+8y
Simplify the radical expression
More Steps


Evaluate
16+8y
Factor the expression
8(2+y)
The root of a product is equal to the product of the roots of each factor
8×2+y
Evaluate the root
More Steps


Evaluate
8
Write the expression as a product where the root of one of the factors can be evaluated
4×2
Write the number in exponential form with the base of 2
22×2
The root of a product is equal to the product of the roots of each factor
22×2
Reduce the index of the radical and exponent with 2
22
22×2+y
Calculate the product
More Steps


Evaluate
2×2+y
The product of roots with the same index is equal to the root of the product
2(2+y)
Calculate the product
4+2y
24+2y
x=48±24+2y
Separate the equation into 2 possible cases
x=48+24+2yx=48−24+2y
Simplify the expression
More Steps


Evaluate
x=48+24+2y
Divide the terms
More Steps


Evaluate
48+24+2y
Rewrite the expression
42(4+4+2y)
Cancel out the common factor 2
24+4+2y
x=24+4+2y
x=24+4+2yx=48−24+2y
Solution
More Steps


Evaluate
x=48−24+2y
Divide the terms
More Steps


Evaluate
48−24+2y
Rewrite the expression
42(4−4+2y)
Cancel out the common factor 2
24−4+2y
x=24−4+2y
x=24+4+2yx=24−4+2y
Show Solution

Rewrite the equation
r=4cos2(θ)sin(θ)+8cos(θ)−1+15cos2(θ)+8sin(2θ)r=4cos2(θ)sin(θ)+8cos(θ)+1+15cos2(θ)+8sin(2θ)
Evaluate
y=2(x−3)(x−1)
Move the expression to the left side
y−2x2+8x=6
To convert the equation to polar coordinates,substitute x for rcos(θ) and y for rsin(θ)
sin(θ)×r−2(cos(θ)×r)2+8cos(θ)×r=6
Factor the expression
−2cos2(θ)×r2+(sin(θ)+8cos(θ))r=6
Subtract the terms
−2cos2(θ)×r2+(sin(θ)+8cos(θ))r−6=6−6
Evaluate
−2cos2(θ)×r2+(sin(θ)+8cos(θ))r−6=0
Solve using the quadratic formula
r=−4cos2(θ)−sin(θ)−8cos(θ)±(sin(θ)+8cos(θ))2−4(−2cos2(θ))(−6)
Simplify
r=−4cos2(θ)−sin(θ)−8cos(θ)±1+15cos2(θ)+8sin(2θ)
Separate the equation into 2 possible cases
r=−4cos2(θ)−sin(θ)−8cos(θ)+1+15cos2(θ)+8sin(2θ)r=−4cos2(θ)−sin(θ)−8cos(θ)−1+15cos2(θ)+8sin(2θ)
Use b−a=−ba=−ba to rewrite the fraction
r=4cos2(θ)sin(θ)+8cos(θ)−1+15cos2(θ)+8sin(2θ)r=−4cos2(θ)−sin(θ)−8cos(θ)−1+15cos2(θ)+8sin(2θ)
Solution
r=4cos2(θ)sin(θ)+8cos(θ)−1+15cos2(θ)+8sin(2θ)r=4cos2(θ)sin(θ)+8cos(θ)+1+15cos2(θ)+8sin(2θ)
Show Solution

Graph