Solve y^2-x=0 - ScanMath

Question

Identify the conic

Find the standard equation of the parabola

Find the vertex of the parabola

Find the focus of the parabola

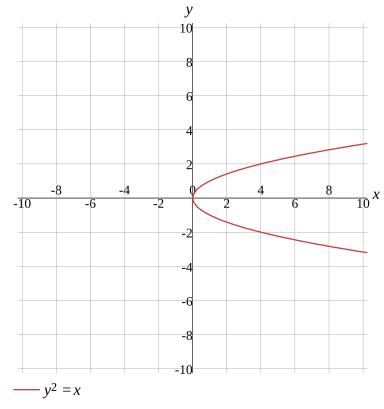
y^{2} = x

Evaluate

y^{2} - x = 0

Move the expression to the right-hand side and change its sign

y^{2} = 0 - (- x)

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

y^{2} = 0 + x

Solution

y^{2} = x

Show Solution

Solve the equation

Solve for x

Solve for y

x = y^{2}

Evaluate

y^{2} - x = 0

Move the expression to the right-hand side and change its sign

- x = 0 - y^{2}

Removing 0 doesn't change the value,so remove it from the expression

- x = - y^{2}

Solution

x = y^{2}

Show Solution

Testing for symmetry

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Not symmetry with respect to the origin

Evaluate

y^{2} - x = 0

To test if the graph of y^{2} - x = 0 is symmetry with respect to the origin,substitute -x for x and -y for y

(- y)^{2} - (- x) = 0

Evaluate

More Steps

Evaluate

(- y)^{2} - (- x)

Rewrite the expression

(- y)^{2} + x

Rewrite the expression

y^{2} + x

y^{2} + x = 0

Solution

Not symmetry with respect to the origin

Show Solution

Find the first derivative

Find the derivative with respect to x

Find the derivative with respect to y

\frac{d y}{d x} = \frac{1}{2 y}

Calculate

y^{2} - x = 0

Take the derivative of both sides

\frac{d}{d x} (y^{2} - x) = \frac{d}{d x} (0)

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (y^{2} - x)

Use differentiation rules

\frac{d}{d x} (y^{2}) + \frac{d}{d x} (- x)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (y^{2})

Use differentiation rules

\frac{d}{d y} (y^{2}) \times \frac{d y}{d x}

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

2 y \frac{d y}{d x}

2 y \frac{d y}{d x} + \frac{d}{d x} (- x)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (- x)

Use differentiation rule \frac{d}{d x} (c f (x)) = c \times \frac{d}{d x} (f (x))

- \frac{d}{d x} (x)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

- 1

2 y \frac{d y}{d x} - 1

2 y \frac{d y}{d x} - 1 = \frac{d}{d x} (0)

Calculate the derivative

2 y \frac{d y}{d x} - 1 = 0

Move the constant to the right-hand side and change its sign

2 y \frac{d y}{d x} = 0 + 1

Removing 0 doesn't change the value,so remove it from the expression

2 y \frac{d y}{d x} = 1

Divide both sides

\frac{2 y \frac{d y}{d x}}{2 y} = \frac{1}{2 y}

Solution

\frac{d y}{d x} = \frac{1}{2 y}

Show Solution

Find the second derivative

Find the second derivative with respect to x

Find the second derivative with respect to y

\frac{d ^{2} y}{d x ^{2}} = - \frac{1}{4 y ^{3}}

Calculate

y^{2} - x = 0

Take the derivative of both sides

\frac{d}{d x} (y^{2} - x) = \frac{d}{d x} (0)

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (y^{2} - x)

Use differentiation rules

\frac{d}{d x} (y^{2}) + \frac{d}{d x} (- x)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (y^{2})

Use differentiation rules

\frac{d}{d y} (y^{2}) \times \frac{d y}{d x}

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

2 y \frac{d y}{d x}

2 y \frac{d y}{d x} + \frac{d}{d x} (- x)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (- x)

Use differentiation rule \frac{d}{d x} (c f (x)) = c \times \frac{d}{d x} (f (x))

- \frac{d}{d x} (x)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

- 1

2 y \frac{d y}{d x} - 1

2 y \frac{d y}{d x} - 1 = \frac{d}{d x} (0)

Calculate the derivative

2 y \frac{d y}{d x} - 1 = 0

Move the constant to the right-hand side and change its sign

2 y \frac{d y}{d x} = 0 + 1

Removing 0 doesn't change the value,so remove it from the expression

2 y \frac{d y}{d x} = 1

Divide both sides

\frac{2 y \frac{d y}{d x}}{2 y} = \frac{1}{2 y}

Divide the numbers

\frac{d y}{d x} = \frac{1}{2 y}

Take the derivative of both sides

\frac{d}{d x} (\frac{d y}{d x}) = \frac{d}{d x} (\frac{1}{2 y})

Calculate the derivative

\frac{d ^{2} y}{d x ^{2}} = \frac{d}{d x} (\frac{1}{2 y})

Use differentiation rules

\frac{d ^{2} y}{d x ^{2}} = \frac{1}{2} \times \frac{d}{d x} (\frac{1}{y})

Rewrite the expression in exponential form

\frac{d ^{2} y}{d x ^{2}} = \frac{1}{2} \times \frac{d}{d x} (y^{- 1})

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (y^{- 1})

Use differentiation rules

\frac{d}{d y} (y^{- 1}) \times \frac{d y}{d x}

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

- y^{- 2} \frac{d y}{d x}

\frac{d ^{2} y}{d x ^{2}} = \frac{1}{2} (- y^{- 2} \frac{d y}{d x})

Rewrite the expression

\frac{d ^{2} y}{d x ^{2}} = \frac{1}{2} (- \frac{\frac{d y}{d x}}{y ^{2}})

Calculate

\frac{d ^{2} y}{d x ^{2}} = - \frac{\frac{d y}{d x}}{2 y ^{2}}

Use equation \frac{d y}{d x} = \frac{1}{2 y} to substitute

\frac{d ^{2} y}{d x ^{2}} = - \frac{\frac{1}{2 y}}{2 y ^{2}}

Solution

More Steps

Calculate

- \frac{\frac{1}{2 y}}{2 y ^{2}}

Divide the terms

More Steps

Evaluate

\frac{\frac{1}{2 y}}{2 y ^{2}}

Multiply by the reciprocal

\frac{1}{2 y} \times \frac{1}{2 y ^{2}}

Multiply the terms

\frac{1}{2 y \times 2 y ^{2}}

Multiply the terms

\frac{1}{4 y ^{3}}

- \frac{1}{4 y ^{3}}

\frac{d ^{2} y}{d x ^{2}} = - \frac{1}{4 y ^{3}}

Show Solution

Rewrite the equation

r = 0 r = \frac{cos ( θ )}{sin ^{2} ( θ )}

Evaluate

y^{2} - x = 0

To convert the equation to polar coordinates,substitute x for r cos (θ) and y for r sin (θ)

(sin (θ) \times r)^{2} - cos (θ) \times r = 0

Factor the expression

sin^{2} (θ) \times r^{2} - cos (θ) \times r = 0

Factor the expression

r (sin^{2} (θ) \times r - cos (θ)) = 0

When the product of factors equals 0,at least one factor is 0

r = 0 sin^{2} (θ) \times r - cos (θ) = 0

Solution

More Steps

Factor the expression

sin^{2} (θ) \times r - cos (θ) = 0

Subtract the terms

sin^{2} (θ) \times r - cos (θ) - (- cos (θ)) = 0 - (- cos (θ))

Evaluate

sin^{2} (θ) \times r = cos (θ)

Divide the terms

r = \frac{cos ( θ )}{sin ^{2} ( θ )}

r = 0 r = \frac{cos ( θ )}{sin ^{2} ( θ )}

Show Solution

Identify the conic

Solve the equation

Testing for symmetry

Find the first derivative

Find the second derivative

Rewrite the equation

Graph