Algebra
Calculus
Trigonometry
Matrix
Question
Solve the equation
α=2π+kπ,k∈Z
Alternative Form
α=90∘+180∘k,k∈Z
Evaluate
sec(α)tan2(α)+1=sec(α)
Find the domain
More Steps
Evaluate
{α=2π+kπ,k∈Zsec(α)=0
Calculate
{α=2π+kπ,k∈Zα∈R
Find the intersection
α=2π+kπ,k∈Z
sec(α)tan2(α)+1=sec(α),α=2π+kπ,k∈Z
Use tan2(x)=sec2(x)−1 to rewrite the expression
sec(α)=sec(α)
Cancel equal terms on both sides of the expression
0=0
The statement is true for any value of α
α∈R
Check if the solution is in the defined range
α∈R,α=2π+kπ,k∈Z
Solution
α=2π+kπ,k∈Z
Alternative Form
α=90∘+180∘k,k∈Z
Show Solution
Verify the identity
true
Evaluate
sec(α)tan2(α)+1=sec(α)
Start working on the left-hand side
More Steps
Evaluate
sec(α)tan2(α)+1
Use tant=costsint to transform the expression
sec(α)(cos(α)sin(α))2+1
Rewrite the expression
More Steps
Evaluate
(cos(α)sin(α))2+1
Rewrite the expression
cos2(α)sin2(α)+1
Reduce fractions to a common denominator
cos2(α)sin2(α)+cos2(α)cos2(α)
Write all numerators above the common denominator
cos2(α)sin2(α)+cos2(α)
sec(α)cos2(α)sin2(α)+cos2(α)
Multiply by the reciprocal
cos2(α)sin2(α)+cos2(α)×sec(α)1
Multiply the terms
cos2(α)sec(α)sin2(α)+cos2(α)
Transform the expression
More Steps
Evaluate
cos2(α)sec(α)
Use sect=cost1 to transform the expression
cos2(α)×cos(α)1
Cancel out the common factor cos(α)
cos(α)
cos(α)sin2(α)+cos2(α)
Use sin2(t)+cos2(t)=1 to transform the expression
cos(α)1
cos(α)1=sec(α)
Start working on the right-hand side
cos(α)1=cos(α)1
Solution
true
Show Solution
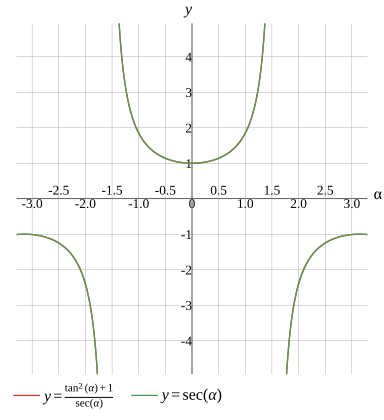
Graph
