Solve using the substitution method of \left\{ \begin{array} { c } { \sqrt{x} + \sqrt{y} = 6 } \\ { \sqrt{x y} = 8 } \end{array} \right.

\begin{align}&\left(x_{1},y_{1}\right) = \left(16,4\right)\\&\left(x_{2},y_{2}\right) = \left(4,16\right)\end{align}

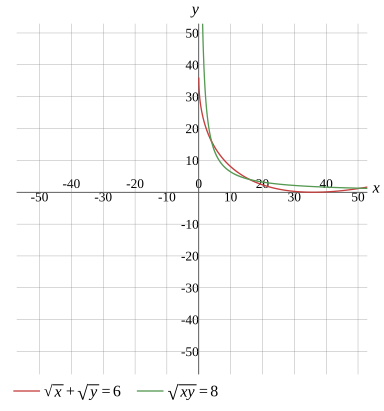
Question :

begin{array c sqrt{x + sqrty = 6 } sqrt{x y = 8 } endarray .

(x_{1}, y_{1}) = (16, 4) (x_{2}, y_{2}) = (4, 16)

Evaluate

{x + y = 6 x y = 8

Solve the equation for x

More Steps

{x = 36 - 12 y + y x y = 8

Substitute the given value of x into the equation x y = 8

(36 - 12 y + y) y = 8

Simplify

More Steps

6 y - y = 8

Move the variable to the right-hand side and change its sign

6 y = 8 + y

Rewrite the expression

y = \frac{8 + y}{6}

Evaluate

y = \frac{8 + y}{6}, \frac{8 + y}{6} \geq 0

Evaluate

More Steps

y = \frac{8 + y}{6}, y \geq - 8

Solve the equation for y

More Steps

y = 16 \cup y = 4, y \geq - 8

Find the intersection

y = 16 \cup y = 4

Rearrange the terms

{x = 36 - 12 y + y y = 16 \cup {x = 36 - 12 y + y y = 4

Calculate

More Steps

{x = 4 y = 16 \cup {x = 36 - 12 y + y y = 4

Calculate

More Steps

{x = 4 y = 16 \cup {x = 16 y = 4

Calculate

{x = 16 y = 4 \cup {x = 4 y = 16

Check the solution

More Steps

{x = 16 y = 4 \cup {x = 4 y = 16

Check the solution

More Steps

{x = 16 y = 4 \cup {x = 4 y = 16

Solution

(x_{1}, y_{1}) = (16, 4) (x_{2}, y_{2}) = (4, 16)

Show Solution