Question
Resuelve la ecuación
θ=kπ,k∈Z
Forma alternativa
θ=180∘k,k∈Z
Evalúe
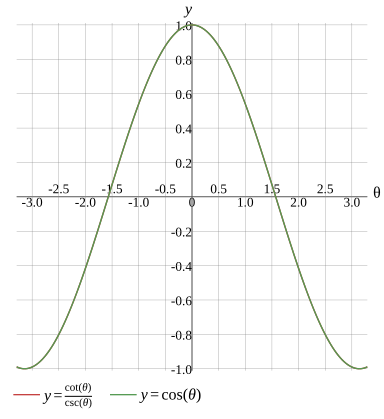
csc(θ)cot(θ)=cos(θ)
Encuentra el dominio
More Steps

Evalúe
{θ=kπ,k∈Zcsc(θ)=0
Calcular
{θ=kπ,k∈Zθ∈R
Encuentra la intersección
θ=kπ,k∈Z
csc(θ)cot(θ)=cos(θ),θ=kπ,k∈Z
Reescribe la expresión
sin(θ)1sin(θ)cos(θ)=cos(θ)
Simplifica la expresión
sin(θ)cos(θ)sin(θ)=cos(θ)
Reducir la fracción
cos(θ)=cos(θ)
La declaracioˊn es verdadera para cualquier valor de θ
θ∈R
Compruebe si la solución está en el rango definido.
θ∈R,θ=kπ,k∈Z
Solution
θ=kπ,k∈Z
Forma alternativa
θ=180∘k,k∈Z
Show Solution

Verificar la identidad
true
Evalúe
csc(θ)cot(θ)=cos(θ)
Empezar a trabajar en el lado izquierdo
More Steps

Evalúe
csc(θ)cot(θ)
Usa cott=sintcost para transformar la expresioˊn
csc(θ)sin(θ)cos(θ)
Multiplica por el recíproco
sin(θ)cos(θ)×csc(θ)1
Multiplica los términos
sin(θ)csc(θ)cos(θ)
Transforma la expresión
More Steps

Evalúe
sin(θ)csc(θ)
Usa csct=sint1 para transformar la expresioˊn
sin(θ)×sin(θ)1
Cancelar el factor comuˊn sin(θ)
1×1
Multiplica los términos
1
1cos(θ)
Divide los términos
cos(θ)
cos(θ)=cos(θ)
Solution
true
Show Solution

Graph