Question
Identifique a cônica
Encontre a equação padrão do círculo
Encontre o raio do círculo
Encontre o centro do círculo
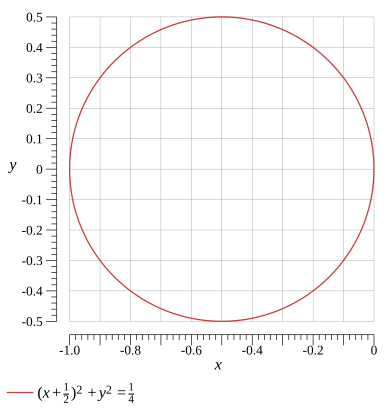
(x+21)2+y2=41
Calcule
x2+y2+x=0
Use a propriedade comutativa para reordenar os termos
x2+x+y2=0
Para completar o quadrado, o mesmo valor precisa ser adicionado a ambos os lados
x2+x+41+y2=41
Solution
(x+21)2+y2=41
Show Solution

Resolva a equação
Resolva para x
Resolva para y
x=2−1+1−4y2x=−21+1−4y2
Calcule
x2+y2+x=0
Reescrever na forma padrão
x2+x+y2=0
Substitua a=1,b=1 ec=y2 na foˊrmula quadraˊtica x=2a−b±b2−4ac
x=2−1±12−4y2
1 elevado a qualquer potência é igual a 1
x=2−1±1−4y2
Separe a equac¸a˜o em 2 casos possıˊveis
x=2−1+1−4y2x=2−1−1−4y2
Solution
x=2−1+1−4y2x=−21+1−4y2
Show Solution

Teste de simetria
Teste de simetria sobre a origem
Testando a simetria em torno do eixo x
Testando a simetria sobre o eixo y
Not symmetry with respect to the origin
Calcule
x2+y2+x=0
Para testar se o graˊfico de x2+y2+x=0 eˊ simetria em relac¸a˜o aˋ origem, substitua -x por x e -y por y
(−x)2+(−y)2−x=0
Calcule
More Steps

Calcule
(−x)2+(−y)2−x
Reescrever a expressão
x2+(−y)2−x
Reescrever a expressão
x2+y2−x
x2+y2−x=0
Solution
Not symmetry with respect to the origin
Show Solution

Encontre a primeira derivada
Encontre a derivada em relac¸a˜o a x
Encontre a derivada em relac¸a˜o a y
dxdy=−2y2x+1
Calcular
x2+y2+x=0
Derivando os dois lados
dxd(x2+y2+x)=dxd(0)
Calcule a derivada
More Steps

Calcule
dxd(x2+y2+x)
Use regras de diferenciação
dxd(x2)+dxd(y2)+dxd(x)
Use dxdxn=nxn−1 para encontrar derivada
2x+dxd(y2)+dxd(x)
Calcule a derivada
More Steps

Calcule
dxd(y2)
Use regras de diferenciação
dyd(y2)×dxdy
Use dxdxn=nxn−1 para encontrar derivada
2ydxdy
2x+2ydxdy+dxd(x)
Use dxdxn=nxn−1 para encontrar derivada
2x+2ydxdy+1
2x+2ydxdy+1=dxd(0)
Calcule a derivada
2x+2ydxdy+1=0
Mova a expressão para o lado direito e mude seu sinal
2ydxdy=0−(2x+1)
Subtraia os termos
More Steps

Calcule
0−(2x+1)
Se um sinal negativo ou um símbolo de subtração aparecer fora dos parênteses, remova os parênteses e altere o sinal de cada termo dentro dos parênteses
0−2x−1
Remover 0 não altera o valor, portanto, remova-o da expressão
−2x−1
2ydxdy=−2x−1
Divida ambos os lados
2y2ydxdy=2y−2x−1
Divida os números
dxdy=2y−2x−1
Solution
dxdy=−2y2x+1
Show Solution

Encontre a segunda derivada
Encontre a segunda derivada em relac¸a˜o a x
Encontre a segunda derivada em relac¸a˜o a y
dx2d2y=−4y34y2+4x2+4x+1
Calcular
x2+y2+x=0
Derivando os dois lados
dxd(x2+y2+x)=dxd(0)
Calcule a derivada
More Steps

Calcule
dxd(x2+y2+x)
Use regras de diferenciação
dxd(x2)+dxd(y2)+dxd(x)
Use dxdxn=nxn−1 para encontrar derivada
2x+dxd(y2)+dxd(x)
Calcule a derivada
More Steps

Calcule
dxd(y2)
Use regras de diferenciação
dyd(y2)×dxdy
Use dxdxn=nxn−1 para encontrar derivada
2ydxdy
2x+2ydxdy+dxd(x)
Use dxdxn=nxn−1 para encontrar derivada
2x+2ydxdy+1
2x+2ydxdy+1=dxd(0)
Calcule a derivada
2x+2ydxdy+1=0
Mova a expressão para o lado direito e mude seu sinal
2ydxdy=0−(2x+1)
Subtraia os termos
More Steps

Calcule
0−(2x+1)
Se um sinal negativo ou um símbolo de subtração aparecer fora dos parênteses, remova os parênteses e altere o sinal de cada termo dentro dos parênteses
0−2x−1
Remover 0 não altera o valor, portanto, remova-o da expressão
−2x−1
2ydxdy=−2x−1
Divida ambos os lados
2y2ydxdy=2y−2x−1
Divida os números
dxdy=2y−2x−1
Use b−a=−ba=−ba para reescrever a frac¸a˜o
dxdy=−2y2x+1
Derivando os dois lados
dxd(dxdy)=dxd(−2y2x+1)
Calcule a derivada
dx2d2y=dxd(−2y2x+1)
Use regras de diferenciação
dx2d2y=−(2y)2dxd(2x+1)×2y−(2x+1)×dxd(2y)
Calcule a derivada
More Steps

Calcule
dxd(2x+1)
Use regras de diferenciação
dxd(2x)+dxd(1)
Calcule a derivada
2+dxd(1)
Use dxd(c)=0 para encontrar derivada
2+0
Calcule
2
dx2d2y=−(2y)22×2y−(2x+1)×dxd(2y)
Calcule a derivada
More Steps

Calcule
dxd(2y)
Simplificar
2×dxd(y)
Calcular
2dxdy
dx2d2y=−(2y)22×2y−(2x+1)×2dxdy
Calcular
dx2d2y=−(2y)24y−(2x+1)×2dxdy
Calcular
More Steps

Calcule
(2x+1)×2dxdy
Aplicar a propriedade distributiva
2x×2dxdy+1×2dxdy
Multiplique os números
4xdxdy+1×2dxdy
Qualquer expressão multiplicada por 1 permanece a mesma
4xdxdy+2dxdy
dx2d2y=−(2y)24y−(4xdxdy+2dxdy)
Se um sinal negativo ou um símbolo de subtração aparecer fora dos parênteses, remova os parênteses e altere o sinal de cada termo dentro dos parênteses
dx2d2y=−(2y)24y−4xdxdy−2dxdy
Calcular
More Steps

Calcule
(2y)2
Calcular a potência
22y2
Calcular a potência
4y2
dx2d2y=−4y24y−4xdxdy−2dxdy
Calcular
dx2d2y=−2y22y−2xdxdy−dxdy
Use a equac¸a˜o dxdy=−2y2x+1 para substituir
dx2d2y=−2y22y−2x(−2y2x+1)−(−2y2x+1)
Solution
More Steps

Calcular
−2y22y−2x(−2y2x+1)−(−2y2x+1)
Multiplicar
More Steps

Multiplique os termos
−2x(−2y2x+1)
Qualquer expressão multiplicada por 1 permanece a mesma
2x×2y2x+1
Cancele o fator comum 2
x×y2x+1
Multiplique os termos
yx(2x+1)
−2y22y+yx(2x+1)−(−2y2x+1)
Calcular a soma ou diferença
More Steps

Calcule
2y+yx(2x+1)−(−2y2x+1)
Simplificar
2y+yx(2x+1)+2y2x+1
Reduza as frações a um denominador comum
2y2y×2y+y×2x(2x+1)×2+2y2x+1
Use a propriedade comutativa para reordenar os termos
2y2y×2y+2yx(2x+1)×2+2y2x+1
Escreva todos os numeradores acima do denominador comum
2y2y×2y+x(2x+1)×2+2x+1
Multiplique os termos
2y4y2+x(2x+1)×2+2x+1
Multiplique os termos
2y4y2+4x2+2x+2x+1
Some os termos
2y4y2+4x2+4x+1
−2y22y4y2+4x2+4x+1
Divida os termos
More Steps

Calcule
2y22y4y2+4x2+4x+1
Multiplique pelo recíproco
2y4y2+4x2+4x+1×2y21
Multiplique os termos
2y×2y24y2+4x2+4x+1
Multiplique os termos
4y34y2+4x2+4x+1
−4y34y2+4x2+4x+1
dx2d2y=−4y34y2+4x2+4x+1
Show Solution

Reescreva a equação
r=0r=−cos(θ)
Calcule
x2+y2+x=0
Para converter a equac¸a˜o em coordenadas polares, substitua rcos(θ) por x e rsin(θ) por y
(cos(θ)×r)2+(sin(θ)×r)2+cos(θ)×r=0
Fatore a expressão
(cos2(θ)+sin2(θ))r2+cos(θ)×r=0
Simplifique a expressão
r2+cos(θ)×r=0
Fatore a expressão
r(r+cos(θ))=0
Quando o produto dos fatores é igual a 0, pelo menos um fator é 0
r=0r+cos(θ)=0
Solution
More Steps

Fatore a expressão
r+cos(θ)=0
Subtraia os termos
r+cos(θ)−cos(θ)=0−cos(θ)
Calcule
r=−cos(θ)
r=0r=−cos(θ)
Show Solution

Graph