Question
Função
Encontre o vértice
Encontre o eixo de simetria
Reescrever na forma de vértice
Load more

(−31,32)
Calcule
y=3x2+2x+1
Encontre a coordenada x do veˊrtice substituindo a=3 e b=2 em x = −2ab
x=−2×32
Resolva a equac¸a˜o para x
x=−31
Encontre a coordenada y do veˊrtice avaliando a func¸a˜o para x=−31
y=3(−31)2+2(−31)+1
Calcular
More Steps

Calcule
3(−31)2+2(−31)+1
Multiplique os termos
More Steps

Calcule
3(−31)2
Calcular a potência
3×91
Multiplique os números
31
31+2(−31)+1
Multiplique os números
More Steps

Calcule
2(−31)
Multiplicar ou dividir um número ímpar de termos negativos é igual a um negativo
−2×31
Multiplique os números
−32
31−32+1
Reduza as frações a um denominador comum
31−32+33
Escreva todos os numeradores acima do denominador comum
31−2+3
Calcular a soma ou diferença
32
y=32
Solution
(−31,32)
Show Solution

Teste de simetria
Teste de simetria sobre a origem
Testando a simetria em torno do eixo x
Testando a simetria sobre o eixo y
Not symmetry with respect to the origin
Calcule
y=3x2+2x+1
Para testar se o graˊfico de y=3x2+2x+1 eˊ simetria em relac¸a˜o aˋ origem, substitua -x por x e -y por y
−y=3(−x)2+2(−x)+1
Simplificar
More Steps

Calcule
3(−x)2+2(−x)+1
Multiplique os termos
3x2+2(−x)+1
Multiplique os números
3x2−2x+1
−y=3x2−2x+1
Mude os sinais de ambos os lados
y=−3x2+2x−1
Solution
Not symmetry with respect to the origin
Show Solution

Identifique a cônica
Encontre a equação padrão da parábola
Encontre o vértice da parábola
Encontre o foco da parábola
Load more

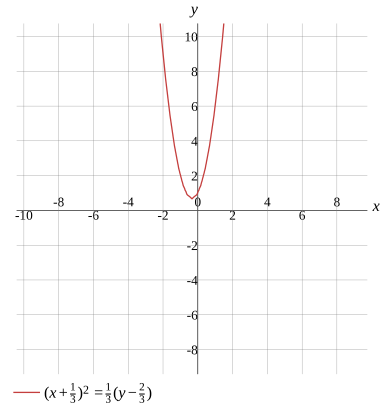
(x+31)2=31(y−32)
Calcule
y=3x2+2x+1
Troque os lados da equação
3x2+2x+1=y
Mova a constante para o lado direito e mude seu sinal
3x2+2x=y−1
Multiplique ambos os lados da equac¸a˜o por 31
(3x2+2x)×31=(y−1)×31
Multiplique os termos
More Steps

Calcule
(3x2+2x)×31
Use a propriedade distributiva para expandir a expressão
3x2×31+2x×31
Multiplique os números
x2+2x×31
Multiplique os números
x2+32x
x2+32x=(y−1)×31
Multiplique os termos
More Steps

Calcule
(y−1)×31
Aplicar a propriedade distributiva
y×31−31
Use a propriedade comutativa para reordenar os termos
31y−31
x2+32x=31y−31
Para completar o quadrado, o mesmo valor precisa ser adicionado a ambos os lados
x2+32x+91=31y−31+91
Use a2+2ab+b2=(a+b)2 para fatorar a expressa˜o
(x+31)2=31y−31+91
Adicione os números
More Steps

Calcule
−31+91
Reduza as frações a um denominador comum
−3×33+91
Multiplique os números
−93+91
Escreva todos os numeradores acima do denominador comum
9−3+1
Adicione os números
9−2
Use b−a=−ba=−ba para reescrever a frac¸a˜o
−92
(x+31)2=31y−92
Solution
(x+31)2=31(y−32)
Show Solution

Resolva a equação
x=3−2+3y−1x=−3−2+3y+1
Calcule
y=3x2+2x+1
Troque os lados da equação
3x2+2x+1=y
Mova a expressão para o lado esquerdo
3x2+2x+1−y=0
Mova a constante para o lado direito
3x2+2x=0−(1−y)
Some os termos
3x2+2x=−1+y
Calcule
x2+32x=3−1+y
Adicione o mesmo valor a ambos os lados
x2+32x+91=3−1+y+91
Calcule
x2+32x+91=9−2+3y
Calcule
(x+31)2=9−2+3y
Pegue a raiz de ambos os lados da equação e lembre-se de usar raízes positivas e negativas
x+31=±9−2+3y
Simplifique a expressão
More Steps

Calcule
9−2+3y
Para tirar a raiz de uma fração, tire a raiz do numerador e do denominador separadamente
9−2+3y
Simplifique a expressão radical
More Steps

Calcule
9
Escreva o nuˊmero na forma exponencial com a base de 3
32
Reduza o ıˊndice da raiz e o expoente com 2
3
3−2+3y
x+31=±3−2+3y
Separe a equac¸a˜o em 2 casos possıˊveis
x+31=3−2+3yx+31=−3−2+3y
Calcular
More Steps

Calcule
x+31=3−2+3y
Mova a constante para o lado direito e mude seu sinal
x=3−2+3y−31
Escreva todos os numeradores acima do denominador comum
x=3−2+3y−1
x=3−2+3y−1x+31=−3−2+3y
Solution
More Steps

Calcule
x+31=−3−2+3y
Mova a constante para o lado direito e mude seu sinal
x=−3−2+3y−31
Subtraia os termos
More Steps

Calcule
−3−2+3y−31
Escreva todos os numeradores acima do denominador comum
3−−2+3y−1
Use b−a=−ba=−ba para reescrever a frac¸a˜o
−3−2+3y+1
x=−3−2+3y+1
x=3−2+3y−1x=−3−2+3y+1
Show Solution

Reescreva a equação
r=6cos2(θ)sin(θ)−2cos(θ)−1−9cos2(θ)−2sin(2θ)r=6cos2(θ)sin(θ)−2cos(θ)+1−9cos2(θ)−2sin(2θ)
Calcule
y=3x2+2x+1
Mova a expressão para o lado esquerdo
y−3x2−2x=1
Para converter a equac¸a˜o em coordenadas polares, substitua rcos(θ) por x e rsin(θ) por y
sin(θ)×r−3(cos(θ)×r)2−2cos(θ)×r=1
Fatore a expressão
−3cos2(θ)×r2+(sin(θ)−2cos(θ))r=1
Subtraia os termos
−3cos2(θ)×r2+(sin(θ)−2cos(θ))r−1=1−1
Calcule
−3cos2(θ)×r2+(sin(θ)−2cos(θ))r−1=0
Resolva usando a fórmula quadrática
r=−6cos2(θ)−sin(θ)+2cos(θ)±(sin(θ)−2cos(θ))2−4(−3cos2(θ))(−1)
Simplificar
r=−6cos2(θ)−sin(θ)+2cos(θ)±1−9cos2(θ)−2sin(2θ)
Separe a equac¸a˜o em 2 casos possıˊveis
r=−6cos2(θ)−sin(θ)+2cos(θ)+1−9cos2(θ)−2sin(2θ)r=−6cos2(θ)−sin(θ)+2cos(θ)−1−9cos2(θ)−2sin(2θ)
Use b−a=−ba=−ba para reescrever a frac¸a˜o
r=6cos2(θ)sin(θ)−2cos(θ)−1−9cos2(θ)−2sin(2θ)r=−6cos2(θ)−sin(θ)+2cos(θ)−1−9cos2(θ)−2sin(2θ)
Solution
r=6cos2(θ)sin(θ)−2cos(θ)−1−9cos2(θ)−2sin(2θ)r=6cos2(θ)sin(θ)−2cos(θ)+1−9cos2(θ)−2sin(2θ)
Show Solution

Graph