Question
Selesaikan persamaan tersebut.
θ=kπ,k∈Z
Bentuk Alternatif
θ=180∘k,k∈Z
Evaluasi
csc(θ)cot(θ)=cos(θ)
Temukan domainnya
More Steps

Evaluasi
{θ=kπ,k∈Zcsc(θ)=0
Menghitung
{θ=kπ,k∈Zθ∈R
Carilah titik perpotongannya
θ=kπ,k∈Z
csc(θ)cot(θ)=cos(θ),θ=kπ,k∈Z
Tulis ulang ungkapan tersebut
sin(θ)1sin(θ)cos(θ)=cos(θ)
Sederhanakan ekspresi tersebut
sin(θ)cos(θ)sin(θ)=cos(θ)
Sederhanakan pecahannya
cos(θ)=cos(θ)
Pernyataan tersebut benar untuk nilai apa pun dari θ
θ∈R
Periksa apakah solusi tersebut berada dalam rentang yang ditentukan.
θ∈R,θ=kπ,k∈Z
Solution
θ=kπ,k∈Z
Bentuk Alternatif
θ=180∘k,k∈Z
Show Solution

Verifikasi identitas
true
Evaluasi
csc(θ)cot(θ)=cos(θ)
Mulailah mengerjakan dari sisi kiri.
More Steps

Evaluasi
csc(θ)cot(θ)
Gunakan cott=sintcost untuk mengubah ekspresi
csc(θ)sin(θ)cos(θ)
Kalikan dengan kebalikannya
sin(θ)cos(θ)×csc(θ)1
Kalikan suku-suku tersebut
sin(θ)csc(θ)cos(θ)
Ubah ekspresi tersebut
More Steps

Evaluasi
sin(θ)csc(θ)
Gunakan csct=sint1 untuk mengubah ekspresi
sin(θ)×sin(θ)1
Hilangkan faktor persekutuan sin(θ)
1×1
Kalikan suku-suku tersebut
1
1cos(θ)
Bagi suku-sukunya
cos(θ)
cos(θ)=cos(θ)
Solution
true
Show Solution

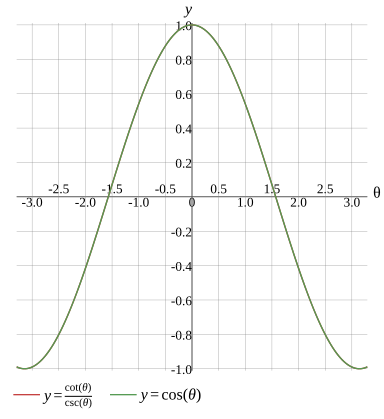
Graph