Question
Решите уравнение
θ=kπ,k∈Z
Альтернативная форма
θ=180∘k,k∈Z
Вычислите
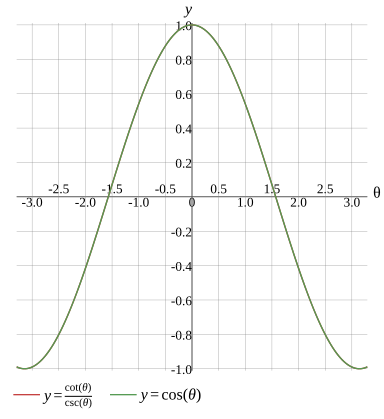
csc(θ)cot(θ)=cos(θ)
Найдите домен
More Steps

Вычислите
{θ=kπ,k∈Zcsc(θ)=0
Рассчитать
{θ=kπ,k∈Zθ∈R
Найдите перекресток
θ=kπ,k∈Z
csc(θ)cot(θ)=cos(θ),θ=kπ,k∈Z
Перепишите выражение
sin(θ)1sin(θ)cos(θ)=cos(θ)
Упростите выражение
sin(θ)cos(θ)sin(θ)=cos(θ)
Уменьшить фракцию
cos(θ)=cos(θ)
Утверждение верно для любого значения θ
θ∈R
Проверить, находится ли решение в заданном диапазоне
θ∈R,θ=kπ,k∈Z
Solution
θ=kπ,k∈Z
Альтернативная форма
θ=180∘k,k∈Z
Show Solution

Подтвердить личность
true
Вычислите
csc(θ)cot(θ)=cos(θ)
Начинайте работать с левой стороны
More Steps

Вычислите
csc(θ)cot(θ)
Используйте cott=sintcost для преобразования выражения
csc(θ)sin(θ)cos(θ)
Умножить на обратную
sin(θ)cos(θ)×csc(θ)1
Умножьте условия
sin(θ)csc(θ)cos(θ)
Преобразуйте выражение
More Steps

Вычислите
sin(θ)csc(θ)
Используйте csct=sint1 для преобразования выражения
sin(θ)×sin(θ)1
Сократите общий делитель sin(θ).
1×1
Умножьте условия
1
1cos(θ)
Разделите члены выражения
cos(θ)
cos(θ)=cos(θ)
Solution
true
Show Solution

Graph